


Next: Combining the evaluations by
Up: Higher order statistics in
Previous: Related Work
Black and white player are playing a game with alternate moves. At
some state 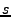 of the game, a play-out analysis means that
of the game, a play-out analysis means that 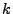 hypothetical
continuations
hypothetical
continuations 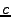 of the game are played out to the end and statistics
from these play outs are used to determine the next move. The
play outs might be sampled by drawing moves from a uniform
distribution over all legal moves, or by other means.
To sample a semi-random move, one can add noise from a random number
generator to a heuristic evaluation of each move and select the best one.
of the game are played out to the end and statistics
from these play outs are used to determine the next move. The
play outs might be sampled by drawing moves from a uniform
distribution over all legal moves, or by other means.
To sample a semi-random move, one can add noise from a random number
generator to a heuristic evaluation of each move and select the best one.
The expected-outcome heuristic 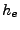 evaluates the move
evaluates the move 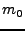 as
as
where 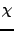 is the indicator function (
is the indicator function (
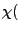 true
true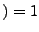 and
and
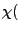 false
false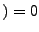 ).
The best move is thus the one that lead to most wins in the play outs
).
The best move is thus the one that lead to most wins in the play outs 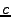 .
.
Note that in Hex and Y the order of moves does not matter. One can
play the game from current state all the way to filling the board. The
winner of the game can be determined from the filled board without
knowing the order of moves. One can think that the single play out
represents all the possible play outs that lead to the same position.
This leads to the all-moves-as-first heuristic 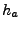 :
:
The best move is the one that lead to wins when used at any point in
the continuation. An example is shown in Figure 3.
Often, play out is done using a semi-random move selection with the heuristic itself.
Figure 3:
The expected-outcome, or equivalently in this case, the
all-moves-as-first heuristic for the first move on a straight (top)
and a bent (bottom) Y board. The colour shows the probability of a
black win assuming random play after the first move. Note that the
straight board gives a large emphasis on the center, which is the
reason why the bent board is often used instead.
|
|
Higher order heuristic 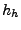 evaluates the move
evaluates the move 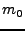 after moves
after moves
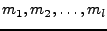 are made in any order.
are made in any order.
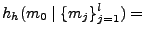 |
|
|
(3) |
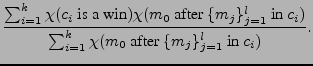 |
|
|
|
The sets of moves
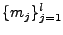 are called patterns. Many
different patterns apply in a future state when sampling a play out,
and one must decide how to combine evaluations corresponding to
different patterns. Also, one has to be selective which patterns are
taken into consideration. Before going into these details, an example
is shown in Figure 4.
are called patterns. Many
different patterns apply in a future state when sampling a play out,
and one must decide how to combine evaluations corresponding to
different patterns. Also, one has to be selective which patterns are
taken into consideration. Before going into these details, an example
is shown in Figure 4.
Figure 4:
The current game state in tic-tac-toe is shown at the top left corner.
Six patterns are numbered and shown in a graph. When
playing out, a state at the bottom right corner is
encountered. Patterns 1, 2, and 4 apply to it.
|
|
Subsections



Next: Combining the evaluations by
Up: Higher order statistics in
Previous: Related Work
Tapani Raiko
2006-09-01
![]() of the game, a play-out analysis means that
of the game, a play-out analysis means that ![]() hypothetical
continuations
hypothetical
continuations ![]() of the game are played out to the end and statistics
from these play outs are used to determine the next move. The
play outs might be sampled by drawing moves from a uniform
distribution over all legal moves, or by other means.
To sample a semi-random move, one can add noise from a random number
generator to a heuristic evaluation of each move and select the best one.
of the game are played out to the end and statistics
from these play outs are used to determine the next move. The
play outs might be sampled by drawing moves from a uniform
distribution over all legal moves, or by other means.
To sample a semi-random move, one can add noise from a random number
generator to a heuristic evaluation of each move and select the best one.
![]() evaluates the move
evaluates the move ![]() as
as
![]() :
:
![\includegraphics[width=0.45\textwidth]{randomanalysis.eps}](img26.png)
![]() evaluates the move
evaluates the move ![]() after moves
after moves
![]() are made in any order.
are made in any order.
![\includegraphics[width=0.4\textwidth]{tictactoe.eps}](img32.png)