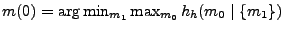Given a state ![]() select a move
select a move ![]() by
by
1: PatternsOn line 3, the moves of the pattern, # of play out
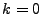
2: Play-out depth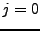
3: Movenoise
4: Make movein state
to get new
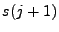
5: Increaseby one
6: Ifnot finished, loop to 3
7: Increaseby one
8: Save movesand the result of
in
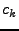
9: Loop to 2 for some time
10: Add new patterns to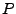
11: Loop to 2 for some time
12: