


Next: Natural Conjugate Gradient
Up: CONJUGATE GRADIENT METHODS
Previous: CONJUGATE GRADIENT METHODS
The extension of the conjugate gradient algorithm to Riemannian
manifolds is done by replacing the gradient with the natural gradient.
The resulting algorithm is known as the Riemannian conjugate gradient
method (Smith, 1993; Edelman et al., 1998).
In principle this extension is relatively simple,
as it is sufficient that all the vector operations take into account
the Riemannian nature of the problem space.
In Riemannian space, the line search should be performed along a geodesic
curve, which is the equivalent of Euclidean straight line.
Additionally, the old gradient vectors
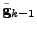 defined in a
different tangent space should be transformed to the tangent space at
the origin of the new gradient by parallel transport along a
geodesic (Smith, 1993). The search direction of the Riemannian conjugate
gradient algorithm is given by
defined in a
different tangent space should be transformed to the tangent space at
the origin of the new gradient by parallel transport along a
geodesic (Smith, 1993). The search direction of the Riemannian conjugate
gradient algorithm is given by
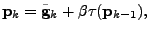 |
(18) |
where
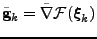 is the natural gradient and
is the natural gradient and
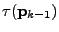 is the previous search direction parallelly transported
to the current search point.
For each iteration, the function is optimized in the search direction
using a line search and the iteration is repeated until satisfactory
convergence is reached.
The multiplier
is the previous search direction parallelly transported
to the current search point.
For each iteration, the function is optimized in the search direction
using a line search and the iteration is repeated until satisfactory
convergence is reached.
The multiplier 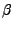 can be computed in multiple different ways.
One popular choice is the Polak-Ribiére
formula (Smith, 1993; Edelman et al., 1998; Nocedal, 1991),
which in Riemannian space is given by
can be computed in multiple different ways.
One popular choice is the Polak-Ribiére
formula (Smith, 1993; Edelman et al., 1998; Nocedal, 1991),
which in Riemannian space is given by
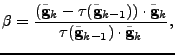 |
(19) |
where
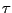 again denotes parallel transport from the previous search point to the
current point.
again denotes parallel transport from the previous search point to the
current point.



Next: Natural Conjugate Gradient
Up: CONJUGATE GRADIENT METHODS
Previous: CONJUGATE GRADIENT METHODS
Tapani Raiko
2007-04-18
![]() defined in a
different tangent space should be transformed to the tangent space at
the origin of the new gradient by parallel transport along a
geodesic (Smith, 1993). The search direction of the Riemannian conjugate
gradient algorithm is given by
defined in a
different tangent space should be transformed to the tangent space at
the origin of the new gradient by parallel transport along a
geodesic (Smith, 1993). The search direction of the Riemannian conjugate
gradient algorithm is given by