Variational Bayesian learning is based on approximating the posterior
distribution
![]() with a tractable approximation
with a tractable approximation
![]() , where
, where
![]() is the data,
is the data,
![]() are the unknown variables
(including both the parameters of the model and the latent variables),
and
are the unknown variables
(including both the parameters of the model and the latent variables),
and
![]() are the (variational) parameters of the approximation. The
approximation is fitted by maximizing a lower bound on marginal
log-likelihood
are the (variational) parameters of the approximation. The
approximation is fitted by maximizing a lower bound on marginal
log-likelihood
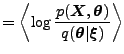 |
(22) | |