


Next: Ensemble Learning
Up: Linear and Nonlinear Factor
Previous: Linear and Nonlinear Factor
According to the general FA model the data has been generated by factors
s through mapping
f:
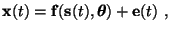 |
|
|
(3) |
where
x is a data vector,
s is a factor vector,
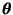 is a parameter vector and
e is a noise vector.
The factors and the noise are assumed to be independent and Gaussian:
is a parameter vector and
e is a noise vector.
The factors and the noise are assumed to be independent and Gaussian:
The linear mapping
f used in FA is
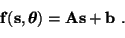 |
(5) |
The model is similar to principal component analysis except that FA
includes the noise term and the factors have a Gaussian distribution.
In NFA, the function
f is allowed to be nonlinear. We use the method
proposed in [6], where the MLP
network
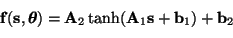 |
(6) |
is used to model the nonlinearity.
The parameter vector
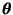 contains both
A and
b.
contains both
A and
b.
In NFA the data is modelled by a high dimensional manifold created
by function
f from a prior Gaussian distribution. It can be compared
to the self-organising map (SOM) [5], but the number
of parameters scale more like in FA. The SOM scales exponentially as
function of the dimensionality of the underlying data manifold. A
small number of parameters keeps the modelled manifold smooth.
We find the parameter vector
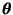 using ensemble learning.
using ensemble learning.



Next: Ensemble Learning
Up: Linear and Nonlinear Factor
Previous: Linear and Nonlinear Factor
Tapani Raiko
2001-09-26
![]() using ensemble learning.
using ensemble learning.