



Next: Nonlinear Factor Analysis
Up: Nonlinear Models
Previous: Self-Organising Map
Supervised Learning Tasks
Nonlinear models have long been used for supervised learning
tasks. The task in supervised learning is to learn a mapping
ffrom observation pairs
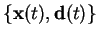 .
The model is
typically written as
.
The model is
typically written as
| y(t) |
= |
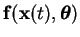 |
(2.11) |
| e(t) |
= |
d(t) - y(t) |
(2.12) |
where
y(t) is the output of the network
f and
e(t) is the error signal or the difference between the
desired response
d(t) and the output
y(t).
The mapping
f has a fixed structure and parameters
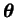 control the actual shape of the mapping. The essential difference to
factor-analysis-like models is that here both the inputs and outputs
are observed. The only hidden variables that have to be learned are
the parameters
control the actual shape of the mapping. The essential difference to
factor-analysis-like models is that here both the inputs and outputs
are observed. The only hidden variables that have to be learned are
the parameters
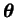 that control the shape of the mapping
f.
that control the shape of the mapping
f.
One of the most common structures for
f is the multilayer
perceptron (MLP) network [5,24] with one hidden
layer defined by
|
y(t) = A1g(A2x(t)+a2) + a1,
|
(2.13) |
where
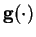 is a nonlinear activation function like the
hyperbolic tangent applied to each component of the vector separately.
It is an universal approximator [26,17], which
means that given enough hidden units, it can approximate any
measurable function to any desired degree of accuracy. The learning
can be done by adjusting the parameters
A and
a so
that the error signal
e(t) gets close to zero. There are
plenty of other structures and methods [24].
is a nonlinear activation function like the
hyperbolic tangent applied to each component of the vector separately.
It is an universal approximator [26,17], which
means that given enough hidden units, it can approximate any
measurable function to any desired degree of accuracy. The learning
can be done by adjusting the parameters
A and
a so
that the error signal
e(t) gets close to zero. There are
plenty of other structures and methods [24].




Next: Nonlinear Factor Analysis
Up: Nonlinear Models
Previous: Self-Organising Map
Tapani Raiko
2001-12-10
![]() .
The model is
typically written as
.
The model is
typically written as
![]() control the actual shape of the mapping. The essential difference to
factor-analysis-like models is that here both the inputs and outputs
are observed. The only hidden variables that have to be learned are
the parameters
control the actual shape of the mapping. The essential difference to
factor-analysis-like models is that here both the inputs and outputs
are observed. The only hidden variables that have to be learned are
the parameters
![]() that control the shape of the mapping
f.
that control the shape of the mapping
f.