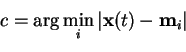Self-Organising Map

The self-organising map (SOM) [39], also known as the Kohonen map, lies in a sense between vector quantisation and nonlinear factor analysis. It operates with map units which are comparable to kernels of mixture models. The map units are organised into a typically two-dimensional grid, where the model vectors of neighbours in the grid are neighbours in the data space.

The actual learning of SOM is done basically as follows. A data sample x(t) is compared to the model vectors m_i and the winner index c(x(t)) is selected with

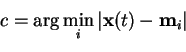$$c = \arg \min_i \left\vert\mathbf{x}(t)-\mathbf{m}_i\right\vert$$ (2.9)

and the model vectors are adjusted towards the data vector

m_i,new=m_i + h(c(x(t)), i)(x(t)-m_i) , (2.10)

where the h is called the neighbourhood function. It is a decreasing function of the distance between the the ith and cth model on the map grid.

If the map grid is just two dimensional, it is useful for visualisation. When the dimensionality gets larger, however, the number of map units grows exponentially and therefore the model is not well suited for tasks with high intrinsic dimensionality. There are plenty of modifications [39] to the basic SOM. The so called generative topographic map [6] is a generative model which is closely related to the SOM.