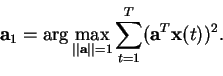Principal Component Analysis

Principal component analysis (PCA)[32,38] also known as the Hotelling transform or the Karhunen-Loève transform is a widely used method for finding the most important directions in the data in the mean-square sense. It is the solution of the FA problem with minimum mean square error and an orthogonal weight matrix.

The first principal component a₁ corresponds to the line on which the projection of the data has the greatest variance:

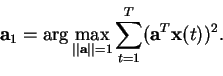$$\mathbf{a}_1 = \arg \max_{\vert\vert\mathbf{a}\vert\vert=1} \sum_{t=1}^T(\mathbf{a}^T\mathbf{x}(t))^2.$$ (2.2)

The other components are found recursively by first removing the projections to the previous principal components:

$$\mathbf{a}_k = \arg \max_{\vert\vert\mathbf{a}\vert\vert=1} \... ...k-1}\mathbf{a}_i \mathbf{a}_i^T \mathbf{x}(t)\right)\right]^2.$$ (2.3)

In practice, the principal components are found by calculating the eigenvectors of the covariance matrix C of the data

$$\mathbf{C} = E\left\{ \mathbf{x}(t)\mathbf{x}(t)^T \right\}$$ (2.4)

The eigenvalues are positive and they correspond to the variances of the projections of data on the eigenvectors.

Principal components can be found in various fields of science. For example, there is an analogy to the physics. If three dimensional data points are considered to be the mass points of a rigid body, the eigenvalues correspond to the principal moments of inertia and the principal components to the principal axes of the body.