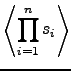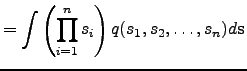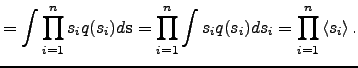Expectations

Equation (20) follows directly from the linearity of the expectation operation, or can be proven analogously to the proof of Equation (23):

$$\left< \prod_{i=1}^n s_i \right> = \int \left(\prod_{i=1}^n s_i\right)q(s_1,s_2,\dots,s_n)d{\mathbf{s}}$$

$$= \int \prod_{i=1}^n s_i q(s_i) d{\mathbf{s}} = \prod_{i=1}^n \int s_i q(s_i) ds_i = \prod_{i=1}^n \left< s_i \right>.$$

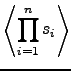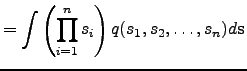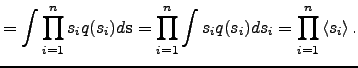Equation (21) states that the variance of a sum of independent variables is the sum of their variances. This fact can be found in basic probability theory books. It can be proven with simple manipulation by using Equations (20) and (23).

Equation (22) can be proven by applying (23) to $\exp s_i$:

$$\left< \exp \left( \sum_{i=1}^n s_i \right) \right> = \left< \prod_{i=1}^n \exp s_i \right> = \prod_{i=1}^n \left< \exp s_i \right>.$$

Equation (24) can be proven by applying Equation (23) to both $s_i$ and $s_i^2$:

$$\mathrm{Var}\left\{\prod_{i=1}^n s_i\right\} = \left< \left(\prod_{i=1}^n s_i\right)^2 \right>-\left< \prod_{j... ...< \prod_{i=1}^n s_i^2 \right> - \left(\prod_{j=1}^n \left< s_j \right>\right)^2$$

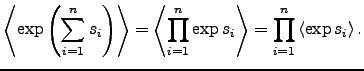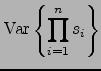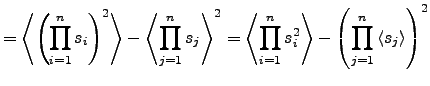$$= \prod_{i=1}^n \left< s_i^2 \right> - \prod_{j=1}^n \left< s_j \... ... + \mathrm{Var}\left\{s_i\right\} \right] - \prod_{j=1}^n \left< s_j \right>^2.$$