Äärellisestä automaatista
muokattu Turingin kone tekee n merkin mittaisella syötteellä
n+1 siirtymää ennen pysähtymistään ((n+1):s siirtymä tarvitaan
loppumerkin havaitsemiseen). Aikavaativuuden suhteen on siis voimassa
![]() .
.
Lisätietoja: Itse asiassa voidaan osoittaa, että
![]() kaikilla vakioilla
kaikilla vakioilla ![]() : äärellinen automaatti
voi pitää sisäisessä tilassaan kirjaa simuloimansa Turingin koneen
työnauhan sisällöstä, jos nauha on rajoitetun pituinen, ja lisäksi
tiedetään että mahdollisuus siirtää syötenauhapäätä myös vasemmalle
ei lisää äärellisten automaattien kielentunnistusvoimaa. Mielenkiintoisempi
tulos on, että
: äärellinen automaatti
voi pitää sisäisessä tilassaan kirjaa simuloimansa Turingin koneen
työnauhan sisällöstä, jos nauha on rajoitetun pituinen, ja lisäksi
tiedetään että mahdollisuus siirtää syötenauhapäätä myös vasemmalle
ei lisää äärellisten automaattien kielentunnistusvoimaa. Mielenkiintoisempi
tulos on, että ![]() peräti kaikilla
peräti kaikilla
![]() . (Luentomuistiinpanojen Lause 1.8.)
. (Luentomuistiinpanojen Lause 1.8.)
Sen sijaan luokka ![]() (ns. ``reaaliaikakielet'')
sisältää muitakin kuin säännöllisiä
kieliä: esimerkiksi palindromikieli
(ns. ``reaaliaikakielet'')
sisältää muitakin kuin säännöllisiä
kieliä: esimerkiksi palindromikieli ![]() on helppo tunnistaa ajassa n+1, mutta on tunnetusti ei-säännöllinen.
on helppo tunnistaa ajassa n+1, mutta on tunnetusti ei-säännöllinen.

Määritellään Turingin koneen M toiminta syötteellä c seuraavasti:
- M laskee funktion arvon t(|c|) ja asettaa aikarajoituslaskurille arvon t(|c|) + 1.
- M simuloi koneen ![]() toimintaa syötteellä c
vähentäen jokaisella
laskenta-askelella aikarajoituslaskuria yhdellä. Jos
toimintaa syötteellä c
vähentäen jokaisella
laskenta-askelella aikarajoituslaskuria yhdellä. Jos ![]() pysähtyy
hyväksyvässä lopputilassa, M hylkää c:n. Jos
pysähtyy
hyväksyvässä lopputilassa, M hylkää c:n. Jos ![]() pysähtyy
hylkäävässä lopputilassa tai aikalaskuri nollautuu, M hyväksyy c:n.
pysähtyy
hylkäävässä lopputilassa tai aikalaskuri nollautuu, M hyväksyy c:n.
Näin määritelty Turingin kone M tunnistaa kielen ![]() . Koska M
pysähtyy kaikilla syötteillä, se on totaalinen. Näin ollen
. Koska M
pysähtyy kaikilla syötteillä, se on totaalinen. Näin ollen ![]() on
rekursiivinen kieli.
on
rekursiivinen kieli.
Oletetaan, että ![]() .
Silloin on olemassa kielen
.
Silloin on olemassa kielen ![]() ajassa t tunnistava Turingin kone N,
joka on sama kuin
ajassa t tunnistava Turingin kone N,
joka on sama kuin ![]() jollakin
jollakin ![]() .
.
Jos ![]() , niin N hyväksyy syötteen d ajassa t(|d|)
ja silloin
, niin N hyväksyy syötteen d ajassa t(|d|)
ja silloin ![]() :n määritelmän mukaan
:n määritelmän mukaan ![]() .
Jos
.
Jos ![]() , niin N hylkää syötteen d
ja silloin
, niin N hylkää syötteen d
ja silloin ![]() :n määritelmän mukaan
:n määritelmän mukaan ![]() .
Ristiriita johtuu oletuksesta, että
.
Ristiriita johtuu oletuksesta, että ![]() DTIME(t).
Siis
DTIME(t).
Siis ![]() DTIME(t).
DTIME(t).
[Lisätieto (PO): Jos funktio t(n) on aikakonstruoituva, niin
kone M saadaan toimimaan ajassa t'(n) millä tahansa
![]() . Tällaisilla funktiopareilla
on siis aina
. Tällaisilla funktiopareilla
on siis aina ![]() .
Lisätekijän
.
Lisätekijän ![]() aiheuttaa se, että koneen M täytyy
simuloida koneen
aiheuttaa se, että koneen M täytyy
simuloida koneen ![]() mielivaltainen nauhamäärä kiinteällä
nauhajoukolla, ja
mielivaltainen nauhamäärä kiinteällä
nauhajoukolla, ja ![]() -luokituksen se, että
tämän lisäksi tarvitsee vielä koneen
-luokituksen se, että
tämän lisäksi tarvitsee vielä koneen ![]() mielivaltainen
nauha-aakkosto koodata M:n kiinteälle aakkostolle.]
mielivaltainen
nauha-aakkosto koodata M:n kiinteälle aakkostolle.]
Todistus.
Kieleen ![]() kuuluvat ne
kuuluvat ne ![]() :n merkkijonot y, joilla f(y) = x.
:n merkkijonot y, joilla f(y) = x.
Olkoon M Turingin kone, joka laskee funktion f polynomisessa ajassa t.
Määritellään Turingin kone ![]() siten, että se laskee syötteellä y M:n
tavoin funktion arvon f(y) ja vertaa sitä x:ään pysähtyen hyväksyvässä
lopputilassa, jos f(y) = x, ja hylkäävässä lopputilassa, jos
siten, että se laskee syötteellä y M:n
tavoin funktion arvon f(y) ja vertaa sitä x:ään pysähtyen hyväksyvässä
lopputilassa, jos f(y) = x, ja hylkäävässä lopputilassa, jos ![]() .
Tämä
.
Tämä ![]() tunnistaa kielen
tunnistaa kielen ![]() . On vielä osoitettava, että
. On vielä osoitettava, että ![]() :n
laskenta tapahtuu polynomisessa ajassa.
:n
laskenta tapahtuu polynomisessa ajassa.
Syötteellä y ![]() laskee f(y):n polynomisessa ajassa ja,
koska
laskee f(y):n polynomisessa ajassa ja,
koska ![]() ,
myös f(y):n vertailu x:ään tapahtuu polynomisessa ajassa.
Siten
,
myös f(y):n vertailu x:ään tapahtuu polynomisessa ajassa.
Siten ![]() . -.5ex
. -.5ex ![]()
Olkoon ![]() ja
ja ![]() P. Laskekoon Turingin kone
P. Laskekoon Turingin kone ![]() syötteellä y M:n tavoin funktion arvon f(y) ja testatkoon sen kuulumisen
kieleen A. Laskenta tapahtuu polynomisessa ajassa, joten
syötteellä y M:n tavoin funktion arvon f(y) ja testatkoon sen kuulumisen
kieleen A. Laskenta tapahtuu polynomisessa ajassa, joten ![]() P.
P.
-
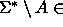 P,
P, -
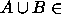 P ja
P ja -
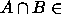 P.
P.
-
Turingin koneesta M saadaan vaihtamalla keskenään sen hyväksyvät ja
hylkäävät lopputilat kielen
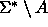 polynomisessa ajassa
tunnistava Turingin kone.
Siten
polynomisessa ajassa
tunnistava Turingin kone.
Siten 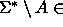 P.
P. -
Määritellään Turingin koneen H toiminta syötteellä x seuraavasti:
- H testaa syötteen kuulumisen kieleen A kuten M. Myönteisessä tapauksessa H pysähtyy hyväksyvässä lopputilassa.
- Muuten H testaa syötteen kuulumisen kieleen B kuten N. Myönteisessä tapauksessa H pysähtyy hyväksyvässä, kielteisessä hylkäävässä lopputilassa.
Näin määritelty Turingin kone H tunnistaa kielen
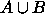 . Tunnistus tapahtuu
polynomisessa ajassa, sillä kumpikin kieli erikseen tunnistetaan polynomisessa
ajassa. Siten
. Tunnistus tapahtuu
polynomisessa ajassa, sillä kumpikin kieli erikseen tunnistetaan polynomisessa
ajassa. Siten 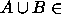 P.
P. -
Väite seuraa edellisistä kohdista, sillä
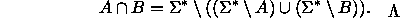
-
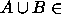 NP ja
NP ja -
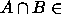 NP.
NP.
-
Määritellään epädeterministisen Turingin koneen H toiminta syötteellä x
seuraavasti:
- H testaa syötteen kuulumisen kieleen A kuten M. Myönteisessä tapauksessa H pysähtyy hyväksyvässä lopputilassa.
- Muuten H testaa syötteen kuulumisen kieleen B kuten N. Myönteisessä tapauksessa H pysähtyy hyväksyvässä, kielteisessä hylkäävässä lopputilassa.
Näin määritelty epädeterministinen Turingin kone H tunnistaa kielen
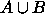 epädeterministisesti. Tunnistus tapahtuu polynomisessa ajassa, sillä kumpikin kieli
erikseen tunnistetaan polynomisessa ajassa. Siten
epädeterministisesti. Tunnistus tapahtuu polynomisessa ajassa, sillä kumpikin kieli
erikseen tunnistetaan polynomisessa ajassa. Siten 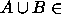 NP.
NP. -
Määritellään epädeterministisen Turingin koneen K toiminta syötteellä x seuraavasti:
- K testaa syötteen kuulumisen kieleen A kuten M. Kielteisessä tapauksessa K pysähtyy hylkäävässä lopputilassa.
- Muuten K testaa syötteen kuulumisen kieleen B kuten N. Myönteisessä tapauksessa K pysähtyy hyväksyvässä, kielteisessä hylkäävässä lopputilassa.
Näin määritelty epädeterministinen Turingin kone K tunnistaa kielen
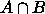 epädeterministisesti. Tunnistus tapahtuu polynomisessa ajassa, sillä kumpikin kieli
erikseen tunnistetaan polynomisessa ajassa. Siten
epädeterministisesti. Tunnistus tapahtuu polynomisessa ajassa, sillä kumpikin kieli
erikseen tunnistetaan polynomisessa ajassa. Siten 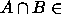 NP. -.5ex
NP. -.5ex 
Todistus. Ensimmäinen väite seuraa tehtävästä 4. Jälkimmäinen todistetaan seuraavasti:
Jos ![]() PSPACE, niin kielen A polynomisessa tilassa tunnistavasta
Turingin koneesta saadaan vaihtamalla keskenään sen hyväksyvät ja hylkäävät
lopputilat kielen
PSPACE, niin kielen A polynomisessa tilassa tunnistavasta
Turingin koneesta saadaan vaihtamalla keskenään sen hyväksyvät ja hylkäävät
lopputilat kielen ![]() polynomisessa tilassa tunnistava
Turingin kone. Siten
polynomisessa tilassa tunnistava
Turingin kone. Siten ![]() PSPACE. -.5ex
PSPACE. -.5ex ![]()
-
Triviaalisti
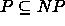 .
.
Jos
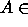 P, niin
P, niin 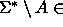 P
P 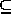 NP, joten
NP, joten 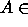 co-NP.
Näin ollen P
co-NP.
Näin ollen P 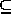 NP
NP  co-NP.
co-NP. -
Kun
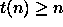 , lauseen 7.5
, lauseen 7.5 mukaan DTIME
mukaan DTIME 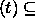 DSPACE(t).
Samalla tavalla samalla ehdolla voidaan päätellä, että NTIME
DSPACE(t).
Samalla tavalla samalla ehdolla voidaan päätellä, että NTIME 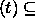 NSPACE(t).
Niinpä NP
NSPACE(t).
Niinpä NP 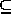 NPSPACE = PSPACE (lauseen 7.10 mukaan).
NPSPACE = PSPACE (lauseen 7.10 mukaan).
Jos
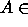 co-NP, niin
co-NP, niin 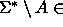 NP
NP 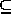 PSPACE, joten
A
PSPACE, joten
A 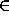 co-PSPACE = PSPACE. Näin ollen NP
co-PSPACE = PSPACE. Näin ollen NP  co-NP
co-NP 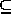 PSPACE.
PSPACE. - Jos P = NP, niin co-NP = co-P = P = NP. Jos NP = PSPACE, niin co-NP = co-PSPACE = PSPACE = NP. Näilllä päättelyillä väitteet todistuvat epäsuorasti.