

Next: Free Form Q
Up: Examples
Previous: Examples
Let us model a set of observations,
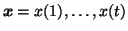 ,
by a
Gaussian distribution parametrised by mean m and log-std
,
by a
Gaussian distribution parametrised by mean m and log-std
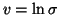 .
We shall approximate the posterior distribution by
q(m,v) =
q(m)q(v), where both q(m) and q(v) are Gaussian. The
parametrisation with log-std is chosen because the posterior of v is
closer to Gaussian than the posterior of
.
We shall approximate the posterior distribution by
q(m,v) =
q(m)q(v), where both q(m) and q(v) are Gaussian. The
parametrisation with log-std is chosen because the posterior of v is
closer to Gaussian than the posterior of 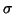 or
or 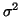 would
be. (Notice that the parametrisation yielding close to Gaussian
posterior distributions is connected to uninformative priors discussed
in section 5.1.)
would
be. (Notice that the parametrisation yielding close to Gaussian
posterior distributions is connected to uninformative priors discussed
in section 5.1.)
Let the priors for m and v be Gaussian with means 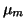 and
and
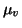 and variances
and variances
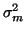 and
and
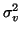 ,
respectively.
The joint density of the observations and the parameters m and vis
,
respectively.
The joint density of the observations and the parameters m and vis
![\begin{displaymath}p(\vec{x}, m, v) = \left[ \prod_t p(x(t) \vert m, v) \right] p(m) p(v) \, .
\end{displaymath}](img82.gif) |
(19) |
As we can see, the posterior is a product of many simple terms.
Let us denote by 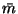 and
and 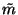 the posterior mean and
variance of m.
the posterior mean and
variance of m.
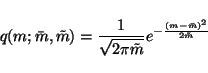 |
(20) |
The distribution
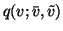 is analogous.
is analogous.
The cost function is now
We see that the cost function has many terms, all of which are
expectations over q(m, v). Since the approximation q(m, v) is
assumed to be factorised into
q(m, v) = q(m) q(v), it is fairly easy
to compute these expectations. For instance, integrating the term
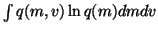 over v yields
over v yields
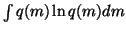 ,
since
,
since 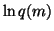 does not depend on v and. Since q(m) is assumed
to be Gaussian with mean
does not depend on v and. Since q(m) is assumed
to be Gaussian with mean 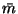 and variance
and variance 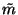 ,
this
integral is, in fact, minus the entropy of a Gaussian distribution and
we have
,
this
integral is, in fact, minus the entropy of a Gaussian distribution and
we have
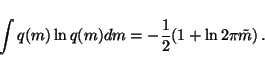 |
(22) |
A similar term, with 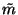 replaced by
replaced by 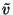 ,
comes from
,
comes from
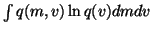 .
.
The terms where expectation is taken over 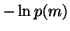 and
and 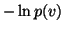 are also simple since
are also simple since
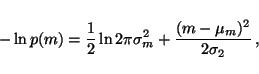 |
(23) |
which means that we only need to be able to compute the expectation of
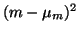 over the Gaussian q(m) having mean
over the Gaussian q(m) having mean 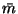 and
variance
and
variance 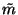 .
This yields
.
This yields
since the variance can be defined by
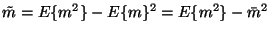 which shows that
which shows that
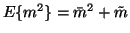 .
Integrating the equation 23 and substituting
equation 24 thus yields
.
Integrating the equation 23 and substituting
equation 24 thus yields
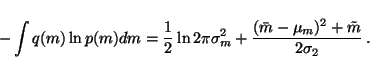 |
(25) |
A similar term, with m replaced by v, will be obtained from
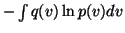 .
.
The last terms are of the form
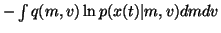 .
Again we will find out that the factorisation
q(m, v) = q(m)
q(v) simplifies the computation of these terms. Recall that x(t)was assumed to be Gaussian with mean m and variance e2v. The
term over which the expectation is taken is thus
.
Again we will find out that the factorisation
q(m, v) = q(m)
q(v) simplifies the computation of these terms. Recall that x(t)was assumed to be Gaussian with mean m and variance e2v. The
term over which the expectation is taken is thus
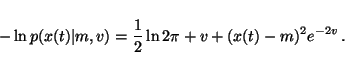 |
(26) |
The expectation over the term
(x(t) - m)2 e-2v is easy to
compute since m and v are assumed to be posteriorly independent.
This means that it is possible to take the expectation separately from
(x(t) - m)2 and e-2v. Using a similar derivation as in
equation 24 yields
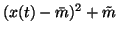 for
the first term. The expectation over e-2v is also fairly easy to
compute:
for
the first term. The expectation over e-2v is also fairly easy to
compute:
This shows that taking expectation over equation 26 yields a term
![\begin{displaymath}-\int q(m, v) \ln p(x(t) \vert m, v) dm dv = \frac{1}{2} \ln ...
...[(x(t) - \bar{m})^2 + \tilde{m}]e^{2\tilde{v} - 2\bar{v}} \, .
\end{displaymath}](img117.gif) |
(28) |
Collecting together all the terms, we obtain the following cost
function
Assuming
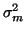 and
and
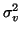 are very large, the minimum of
the cost function can be solved by setting the gradient of the cost
function C to zero. This yields the following:
are very large, the minimum of
the cost function can be solved by setting the gradient of the cost
function C to zero. This yields the following:
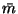 |
= |
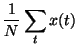 |
(30) |
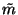 |
= |
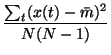 |
(31) |
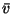 |
= |
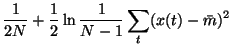 |
(32) |
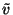 |
= |
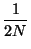 |
(33) |
In case
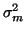 and
and
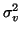 cannot be assumed very large,
the equations for
cannot be assumed very large,
the equations for 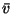 and
and 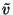 are not that simple, but
the solution can still be obtained by solving the zero-point of the
gradient.
are not that simple, but
the solution can still be obtained by solving the zero-point of the
gradient.
Figure:
Comparison of the true and approximate posterior distributions for a test set containing 100 data points drawn from a model with m=1 and
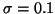 .
The plot on the left shows the true posterior distribution over m and v. The plot on the right shows the approximate posterior distribution consisting of a diagonal Gaussian distribution.
.
The plot on the left shows the true posterior distribution over m and v. The plot on the right shows the approximate posterior distribution consisting of a diagonal Gaussian distribution.
![\includegraphics[width=10.0cm]{prob_contour1.eps}](img131.gif) |
Figure 3 shows a comparison of the true posterior distribution and the approximate posterior. The data set consisted of 100 points drawn from a model with m=1 and
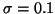 .
The contours in both distributions are centred in the same region, a model that underestimates m.The contours for the two distributions are qualitatively similar although the true distribution is not symmetrical about the mean value of v.
.
The contours in both distributions are centred in the same region, a model that underestimates m.The contours for the two distributions are qualitatively similar although the true distribution is not symmetrical about the mean value of v.


Next: Free Form Q
Up: Examples
Previous: Examples
Harri Lappalainen
2000-03-03
![]() ,
by a
Gaussian distribution parametrised by mean m and log-std
,
by a
Gaussian distribution parametrised by mean m and log-std
![]() .
We shall approximate the posterior distribution by
q(m,v) =
q(m)q(v), where both q(m) and q(v) are Gaussian. The
parametrisation with log-std is chosen because the posterior of v is
closer to Gaussian than the posterior of
.
We shall approximate the posterior distribution by
q(m,v) =
q(m)q(v), where both q(m) and q(v) are Gaussian. The
parametrisation with log-std is chosen because the posterior of v is
closer to Gaussian than the posterior of ![]() or
or ![]() would
be. (Notice that the parametrisation yielding close to Gaussian
posterior distributions is connected to uninformative priors discussed
in section 5.1.)
would
be. (Notice that the parametrisation yielding close to Gaussian
posterior distributions is connected to uninformative priors discussed
in section 5.1.)
![]() and
and
![]() and variances
and variances
![]() and
and
![]() ,
respectively.
The joint density of the observations and the parameters m and vis
,
respectively.
The joint density of the observations and the parameters m and vis
![\begin{displaymath}p(\vec{x}, m, v) = \left[ \prod_t p(x(t) \vert m, v) \right] p(m) p(v) \, .
\end{displaymath}](img82.gif)
![]() and
and ![]() the posterior mean and
variance of m.
the posterior mean and
variance of m.
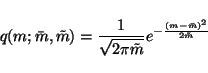
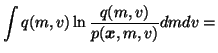
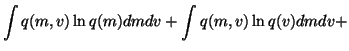
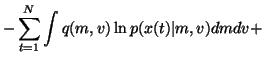
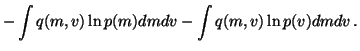
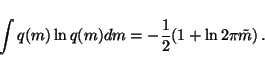
![]() and
and ![]() are also simple since
are also simple since
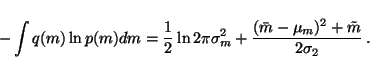
![]() .
Again we will find out that the factorisation
q(m, v) = q(m)
q(v) simplifies the computation of these terms. Recall that x(t)was assumed to be Gaussian with mean m and variance e2v. The
term over which the expectation is taken is thus
.
Again we will find out that the factorisation
q(m, v) = q(m)
q(v) simplifies the computation of these terms. Recall that x(t)was assumed to be Gaussian with mean m and variance e2v. The
term over which the expectation is taken is thus
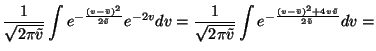
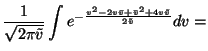
![$\displaystyle \frac{1}{\sqrt{2\pi\tilde{v}}} \int e^{-\frac{[v + (2\tilde{v} -
\bar{v})]^2 + 4\bar{v}\tilde{v} - 4\tilde{v}^2} {2 \tilde{v}}} =$](img115.gif)
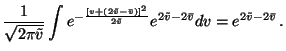
![\begin{displaymath}-\int q(m, v) \ln p(x(t) \vert m, v) dm dv = \frac{1}{2} \ln ...
...[(x(t) - \bar{m})^2 + \tilde{m}]e^{2\tilde{v} - 2\bar{v}} \, .
\end{displaymath}](img117.gif)
![$\displaystyle \sum_{t=1}^N
\frac{1}{2}[(x(t) - \bar{m})^2 + \tilde{m}] e^{2\tilde{v}-2\bar{v}} +
N \bar{v} +$](img119.gif)
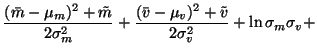
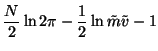
![]() and
and
![]() are very large, the minimum of
the cost function can be solved by setting the gradient of the cost
function C to zero. This yields the following:
are very large, the minimum of
the cost function can be solved by setting the gradient of the cost
function C to zero. This yields the following:
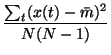
![\includegraphics[width=10.0cm]{prob_contour1.eps}](img131.gif)
![]() .
The contours in both distributions are centred in the same region, a model that underestimates m.The contours for the two distributions are qualitatively similar although the true distribution is not symmetrical about the mean value of v.
.
The contours in both distributions are centred in the same region, a model that underestimates m.The contours for the two distributions are qualitatively similar although the true distribution is not symmetrical about the mean value of v.