Principal component analysis

Principal component analysis (PCA) is a classical statistical method. This linear transform has been widely used in data analysis and compression. The following presentation is adapted from [9]. Some of the texts on the subject also include [30], [31]. Principal component analysis is based on the statistical representation of a random variable. Suppose we have a random vector population x, where

and the mean of that population is denoted by

and the covariance matrix of the same data set is

The components of , denoted by , represent the covariances between the random variable components and . The component is the variance of the component . The variance of a component indicates the spread of the component values around its mean value. If two components and of the data are uncorrelated, their covariance is zero . The covariance matrix is, by definition, always symmetric.

From a sample of vectors , we can calculate the sample mean and the sample covariance matrix as the estimates of the mean and the covariance matrix.

From a symmetric matrix such as the covariance matrix, we can calculate an orthogonal basis by finding its eigenvalues and eigenvectors. The eigenvectors and the corresponding eigenvalues are the solutions of the equation

For simplicity we assume that the are distinct. These values can be found, for example, by finding the solutions of the characteristic equation

where the is the identity matrix having the same order than and the |.| denotes the determinant of the matrix. If the data vector has n components, the characteristic equation becomes of order n. This is easy to solve only if n is small. Solving eigenvalues and corresponding eigenvectors is a non-trivial task, and many methods exist. One way to solve the eigenvalue problem is to use a neural solution to the problem [30]. The data is fed as the input, and the network converges to the wanted solution.

By ordering the eigenvectors in the order of descending eigenvalues (largest first), one can create an ordered orthogonal basis with the first eigenvector having the direction of largest variance of the data. In this way, we can find directions in which the data set has the most significant amounts of energy.

Suppose one has a data set of which the sample mean and the covariance matrix have been calculated. Let be a matrix consisting of eigenvectors of the covariance matrix as the row vectors.

By transforming a data vector x, we get

which is a point in the orthogonal coordinate system defined by the eigenvectors. Components of y can be seen as the coordinates in the orthogonal base. We can reconstruct the original data vector from by

using the property of an orthogonal matrix . The is the transpose of a matrix . The original vector was projected on the coordinate axes defined by the orthogonal basis. The original vector was then reconstructed by a linear combination of the orthogonal basis vectors.

Instead of using all the eigenvectors of the covariance matrix, we may represent the data in terms of only a few basis vectors of the orthogonal basis. If we denote the matrix having the K first eigenvectors as rows by , we can create a similar transformation as seen above

and

This means that we project the original data vector on the coordinate axes having the dimension K and transforming the vector back by a linear combination of the basis vectors. This minimizes the mean-square error between the data and this representation with given number of eigenvectors.

If the data is concentrated in a linear subspace, this provides a way to compress data without losing much information and simplifying the representation. By picking the eigenvectors having the largest eigenvalues we lose as little information as possible in the mean-square sense. One can e.g. choose a fixed number of eigenvectors and their respective eigenvalues and get a consistent representation, or abstraction of the data. This preserves a varying amount of energy of the original data. Alternatively, we can choose approximately the same amount of energy and a varying amount of eigenvectors and their respective eigenvalues. This would in turn give approximately consistent amount of information in the expense of varying representations with regard to the dimension of the subspace.

We are here faced with contradictory goals: On one hand, we should simplify the problem by reducing the dimension of the representation. On the other hand we want to preserve as much as possible of the original information content. PCA offers a convenient way to control the trade-off between loosing information and simplifying the problem at hand.

As it will be noted later, it may be possible to create piecewise linear models by dividing the input data to smaller regions and fitting linear models locally to the data.

Now, consider a small example showing the characteristics of the eigenvectors. Some artificial data has been generated, which is illustrated in the Figure 3.1. The small dots are the points in the data set.

  
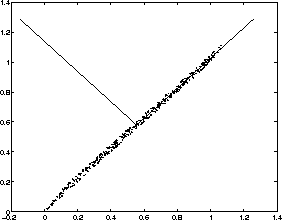
Figure 3.1: Eigenvectors of the artificially created data

Sample mean and sample covariance matrix can easily be calculated from the data. Eigenvectors and eigenvalues can be calculated from the covariance matrix. The directions of eigenvectors are drawn in the Figure as lines. The first eigenvector having the largest eigenvalue points to the direction of largest variance (right and upwards) whereas the second eigenvector is orthogonal to the first one (pointing to left and upwards). In this example the first eigenvalue corresponding to the first eigenvector is while the other eigenvalue is . By comparing the values of eigenvalues to the total sum of eigenvalues, we can get an idea how much of the energy is concentrated along the particular eigenvector. In this case, the first eigenvector contains almost all the energy. The data could be well approximated with a one-dimensional representation.

Sometimes it is desirable to investigate the behavior of the system under small changes. Assume that this system, or phenomenon is constrained to a n-dimensional manifold and can be approximated with a linear manifold. Suppose one has a small change along one of the coordinate axes in the original coordinate system. If the data from the phenomenon is concentrated in a subspace, we can project this small change to the approximative subspace built with PCA by projecting on all the basis vectors in the linear subspace by

where the matrix has the K first eigenvectors as rows. Subspace has then a dimension of K. represents the change caused by the original small change. This can be transformed back with a change of basis by taking a linear combination of the basis vectors by

Then, we get the typical change in the real-world coordinate system caused by a small change by assuming that the phenomenon constrains the system to have values in the limited subspace only.