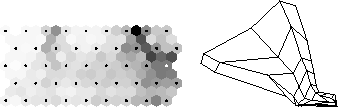
Figure 2.11: U-matrix and Sammon's mapping of the SOM
Self-Organizing Map has proven useful in many technical applications. Many applications have been published in the open literature. Representative examples can be found in an article by Kohonen et al. [22].
In an industrial setting, the SOM has been applied, for example, in process and machine state monitoring [1] [2] [4] [7] [11] [18], fault identification [41] and in robot control [35].
In process and systems analysis, the use of SOM is well motivated [22]. The number of state variables may exceed the number of measurements by an order of magnitude. Also, the state variables may be non-linearly related. In this case, the analystical model of the plant in question would not be identifiable from the measurements.
In fault diagnosis, the SOM has two functions. Firstly, the SOM can be used in detecting the fault and in identifying it. One can detect faults even if there are no measurements of the faulty states by investigating the quantization error between the SOM and the measurements. If the quantization error exceeds a pre-defined limit, a faulty state has occurred. If one needs also to identify faults, representative examples of the faulty situations must have been recorded.
In an application, measurements were made from a computer system in a network environment. The system was measured in terms of utilization rates of the central processing unit and traffic volumes in the network. It was not known a priori what the characteristic states in the operation of the system would be. The SOM was used in clustering data measured from the system, or to form a representation of the characteristic states. Such a representation would be useful in monitoring the current state of the system.

Figure 2.11: U-matrix and Sammon's mapping of the SOM
In the Figure 2.11 the U-matrix representation and the Sammon's mapping of the SOM is presented. These representations reveal the characteristic states of the system. The SOM can in this way be used in monitoring the current state of the system. This kind of monitoring application is based on the ability of SOM to represents the density function of input data on a low-dimensional display [22].
The component plane representation in 2.12 shows the relative component distribution of the measurements. If something is known about the characteristic states of the system, the component planes can help in giving states descriptions, or labels. Then, a mapping from the measurement space to map units is a mapping to a name describing the state.

Figure 2.12: Relative distributions of the measurements in planes representation