|
 Geneettistä algoritmia sovellettaessa ongelman ratkaiseva ohjelma sunnitellaan
moduleiksi siten että modulit ovat valinnaisia. Moduleja edustava perimä
toteutetaan useimmiten laskennallisen hallittavuuden vuoksi binääritaulukkona,
jossa 1 edustaa ominaisuutta ja 0 sen puutetta. Laajoissa ohjelmistoissa perimä
voidaan kuvata tuhansien, jopa kymmenien tuhansien alkioiden taulukolla. Geneettistä algoritmia sovellettaessa ongelman ratkaiseva ohjelma sunnitellaan
moduleiksi siten että modulit ovat valinnaisia. Moduleja edustava perimä
toteutetaan useimmiten laskennallisen hallittavuuden vuoksi binääritaulukkona,
jossa 1 edustaa ominaisuutta ja 0 sen puutetta. Laajoissa ohjelmistoissa perimä
voidaan kuvata tuhansien, jopa kymmenien tuhansien alkioiden taulukolla.
 Taulukon sisältöä muokkaamalla saadaan ohjelman käyttäytyminen muuttumaan.
Ohjelmasta toteutetaan useita kilpailevia versioita ja versioita edustavia
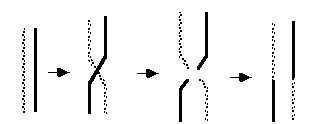
taulukoita monistetaan, risteytetään ja mutatoidaan yksisoluisia jäljittelevällä
tavalla. Ohjelmaversioista karsitaan niiden käyttäytymisen perusteella heikoimmat
ja risteytetään kelpuutetut uudeksi sukupolveksi. Riittävä sukupolvien määrä
tuottaa optimaalisen ratkaisun, mutaatioita tarvitaan vain riittävän versioinnin
ylläpitämiseksi. Taulukon sisältöä muokkaamalla saadaan ohjelman käyttäytyminen muuttumaan.
Ohjelmasta toteutetaan useita kilpailevia versioita ja versioita edustavia
taulukoita monistetaan, risteytetään ja mutatoidaan yksisoluisia jäljittelevällä
tavalla. Ohjelmaversioista karsitaan niiden käyttäytymisen perusteella heikoimmat
ja risteytetään kelpuutetut uudeksi sukupolveksi. Riittävä sukupolvien määrä
tuottaa optimaalisen ratkaisun, mutaatioita tarvitaan vain riittävän versioinnin
ylläpitämiseksi.
 Olen esityksessäni pitäytynyt yksikkömuodossa geneettinen algoritmi, tarkoittaen
alla olevaa pseudokielistä yleistystä. Alan kirjoituksissa termillä tarkoitetaan
toisinaan myös optimoinnin kohteena olevia yksittäisiä sovellus- ja jopa
ratkaisuversioita tässä kuvattavan yleisen mallin lisäksi. Olen esityksessäni pitäytynyt yksikkömuodossa geneettinen algoritmi, tarkoittaen
alla olevaa pseudokielistä yleistystä. Alan kirjoituksissa termillä tarkoitetaan
toisinaan myös optimoinnin kohteena olevia yksittäisiä sovellus- ja jopa
ratkaisuversioita tässä kuvattavan yleisen mallin lisäksi.

- muotoile ongelma
- kehitä karkea ratkaisurakenteiden populaatio
- versioi ja risteytä rakenteet
- evaluoi rakenteet
- karsi rakenteet
- jatka riviltä 3. ellei mikään ratkaisu tyydytä
 Ongelman muotoilu edellyttää ratkaisun erittelyä siltä edellytettävien
ominaisuuksien mukaan, niin että ratkaisun tuottava rakenne voidaan kuvata
perimällä. Alkupopulaatio voidaan tuottaa mutatoimalla ja monistamalla
alkuratkaisua. Ongelman muotoilu edellyttää ratkaisun erittelyä siltä edellytettävien
ominaisuuksien mukaan, niin että ratkaisun tuottava rakenne voidaan kuvata
perimällä. Alkupopulaatio voidaan tuottaa mutatoimalla ja monistamalla
alkuratkaisua.
Yleinen malli
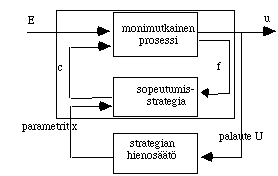
 Yleisellä tasolla geneettisen algoritmin (GA) hakuavaruuden laajuutta voidaan
tarkastella kutsussa GA(N,C,M,G,W,S) olevien kuuden parametrin avulla (Holland).
Parametreista N edustaa populaation yksilöiden määrää eli kokoa. C ilmaisee
risteytyksien suhteellista osuutta, kustakin sukupolvesta risteytetään C*N
yksilöä. C kuten M ja G voi saada arvoja väliltä 0.0-1.0. M määrittää
mutaatioiden esiintymistiheyden, joka saadaan tulosta M*N*L, missä L edustaa
perimän sisältämien geenien määrää. Pieni mutaatioiden osuus varmistaa, ettei
haku juutu paikallisiin optimeihin - suurella mutaatioiden määrällä voidaan
hävittää jo löytynyt ratkaisu. G määrittää seuraavaan sukupolveen selviytyvien
osuuden N*(1-G). W säätelee valintafunktion skaalausta, ts. sillä määritellään se
valintafunktion arvo, joka määrää karsinnan nollapisteen: Jos esimerkiksi
yksilöihin liitetyt painokertoimet voivat saada arvoja välillä 0 - 130, niin
ensimmäisessä sukupolvessa ratkaisujen saamien painokertoimien hajonta on
laajempi kuin satojen sukupolvien jälkeen - kuitenkin populaatioon sovellettavan
karsinnan on tarkasteltava kutakin sukupolvea tasa-arvoisesti. S parametrillä
säädellään sitä pyritäänkö kunkin sukupolven parhaiden ratkaisujen perimä
kopioimaan vai voidaanko se jopa kadottaa risteyttämällä. Edellinen nopeuttaa
optimaalisen ratkaisun löytymistä, jälkimmäinen estää juuttumisen paikallisiin
optimeihin. Yleisellä tasolla geneettisen algoritmin (GA) hakuavaruuden laajuutta voidaan
tarkastella kutsussa GA(N,C,M,G,W,S) olevien kuuden parametrin avulla (Holland).
Parametreista N edustaa populaation yksilöiden määrää eli kokoa. C ilmaisee
risteytyksien suhteellista osuutta, kustakin sukupolvesta risteytetään C*N
yksilöä. C kuten M ja G voi saada arvoja väliltä 0.0-1.0. M määrittää
mutaatioiden esiintymistiheyden, joka saadaan tulosta M*N*L, missä L edustaa
perimän sisältämien geenien määrää. Pieni mutaatioiden osuus varmistaa, ettei
haku juutu paikallisiin optimeihin - suurella mutaatioiden määrällä voidaan
hävittää jo löytynyt ratkaisu. G määrittää seuraavaan sukupolveen selviytyvien
osuuden N*(1-G). W säätelee valintafunktion skaalausta, ts. sillä määritellään se
valintafunktion arvo, joka määrää karsinnan nollapisteen: Jos esimerkiksi
yksilöihin liitetyt painokertoimet voivat saada arvoja välillä 0 - 130, niin
ensimmäisessä sukupolvessa ratkaisujen saamien painokertoimien hajonta on
laajempi kuin satojen sukupolvien jälkeen - kuitenkin populaatioon sovellettavan
karsinnan on tarkasteltava kutakin sukupolvea tasa-arvoisesti. S parametrillä
säädellään sitä pyritäänkö kunkin sukupolven parhaiden ratkaisujen perimä
kopioimaan vai voidaanko se jopa kadottaa risteyttämällä. Edellinen nopeuttaa
optimaalisen ratkaisun löytymistä, jälkimmäinen estää juuttumisen paikallisiin
optimeihin.
 Strategiasta riippuen algoritmin sovellukset voidaan jakaa kahteen pääluokkaan,
sen mukaan mitä perimän avulla kuvataan. Pääsuuntauksia kutsutaan Pittin esim.
(De Jong) ja Michiganin (Holland) versioiksi sen mukaan liitetäänkö yksittäiseen
geeniin kokonaisia proseduureja vai ohjelmalauseita. Strategiasta riippuen algoritmin sovellukset voidaan jakaa kahteen pääluokkaan,
sen mukaan mitä perimän avulla kuvataan. Pääsuuntauksia kutsutaan Pittin esim.
(De Jong) ja Michiganin (Holland) versioiksi sen mukaan liitetäänkö yksittäiseen
geeniin kokonaisia proseduureja vai ohjelmalauseita.
Sovellusesimerkki
 Käytän esimerkkinä yksinkertaistettua optimointiongelmaa - hypermediadokumentin
julkaisumuodon ja ilmiasun valintaa. Tehtävänä on suunnitella geneettistä
algoritmia käsittelevä vuorovaikutteinen hypermediadokumentti. Ensiksi on
päätettävä käytetäänkö dokumentissa 256 väriä vai mustavalkoisuutta,
hinnoitellaanko/tuotetaanko nimike materiaaliltaan 150,- vai 250,- markan
hintaiseksi ja julkaistaanko se CD-ROMina vai levykkeinä. On siis löydettävä
tasapaino tuotteen hyväksyttävyyden/jaeltavuuden, tuotantoon panostettavien
resurssien ja arvioitavan tuoton suhteen. Käytän esimerkkinä yksinkertaistettua optimointiongelmaa - hypermediadokumentin
julkaisumuodon ja ilmiasun valintaa. Tehtävänä on suunnitella geneettistä
algoritmia käsittelevä vuorovaikutteinen hypermediadokumentti. Ensiksi on
päätettävä käytetäänkö dokumentissa 256 väriä vai mustavalkoisuutta,
hinnoitellaanko/tuotetaanko nimike materiaaliltaan 150,- vai 250,- markan
hintaiseksi ja julkaistaanko se CD-ROMina vai levykkeinä. On siis löydettävä
tasapaino tuotteen hyväksyttävyyden/jaeltavuuden, tuotantoon panostettavien
resurssien ja arvioitavan tuoton suhteen.
 Muotoilen aluksi ratkaisulle esitysmallin (representation scheme): iImaistaan
kolmea vaihtoehtoista edellä kuvattua valintaa kaksiaakkosisella {0,1}
merkkijonolla, edustakoon se suunnittelustrategian perimää. Aakkoston koko K on
siis 2 ja perimän pituus (sen geenien lukumäärä) L on 3, ja näin
strategiavaihtoehtoja on 8, K potenssiin L. Muotoilen aluksi ratkaisulle esitysmallin (representation scheme): iImaistaan
kolmea vaihtoehtoista edellä kuvattua valintaa kaksiaakkosisella {0,1}
merkkijonolla, edustakoon se suunnittelustrategian perimää. Aakkoston koko K on
siis 2 ja perimän pituus (sen geenien lukumäärä) L on 3, ja näin
strategiavaihtoehtoja on 8, K potenssiin L.
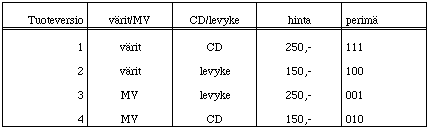
 Koska tarkoituksena on perustaa yrityksen toiminta vuorovaikutteisten
tietokonedokumenttien tuotannolle ja yrityksen näkökulmasta on tärkeätä saavuttaa
kokemusta eri versioiden toteutukseen liittyvistä ongelmista niin päätetään
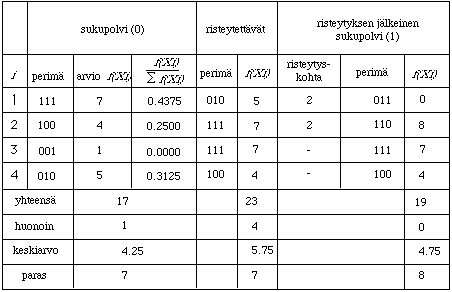
aluksi kokeilla tuotteitten myyntiä neljän vaihtoehtoisen version avulla ja
tarkkailla niiden myyntiä. Tilannetta voidaan tarkastella esimerkiksi seuraavan
mallin avulla. Koska tarkoituksena on perustaa yrityksen toiminta vuorovaikutteisten
tietokonedokumenttien tuotannolle ja yrityksen näkökulmasta on tärkeätä saavuttaa
kokemusta eri versioiden toteutukseen liittyvistä ongelmista niin päätetään
aluksi kokeilla tuotteitten myyntiä neljän vaihtoehtoisen version avulla ja
tarkkailla niiden myyntiä. Tilannetta voidaan tarkastella esimerkiksi seuraavan
mallin avulla.
|
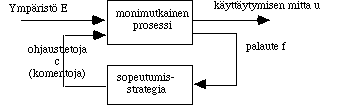
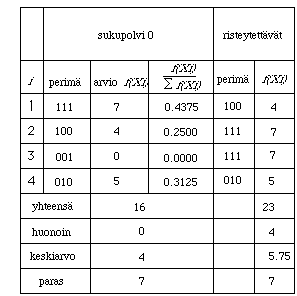
 Geneettinen algoritmi on toistoon perustuva proseduuri, joka ylläpitää
vakiokokoista ehdokasratkaisujen populaatiota P(t). Jokaisen toiston, sukupolven,
aikana populaation sisältämät rakenteet arvioidaan ja arvion perusteella valitaan
ne rakenteet, joista tuotetaan uusi ehdokassukupolvi. Geneettistä algoritmia on
sovellettu mm. kriittisten proseduurien parametrien arvoalueiden optimointiin
kuvaamalla parametrien ennakoitu arvoalue geneettisellä koodilla - risteytys ja
luonnollinen valinta seulovat optimaaliset parametrijoukot. Usein on tarpeen
korvata risteytys sovellukseen paremmin sopivilla lisääntymisrutiineilla.
Geneettinen algoritmi on toistoon perustuva proseduuri, joka ylläpitää
vakiokokoista ehdokasratkaisujen populaatiota P(t). Jokaisen toiston, sukupolven,
aikana populaation sisältämät rakenteet arvioidaan ja arvion perusteella valitaan
ne rakenteet, joista tuotetaan uusi ehdokassukupolvi. Geneettistä algoritmia on
sovellettu mm. kriittisten proseduurien parametrien arvoalueiden optimointiin
kuvaamalla parametrien ennakoitu arvoalue geneettisellä koodilla - risteytys ja
luonnollinen valinta seulovat optimaaliset parametrijoukot. Usein on tarpeen
korvata risteytys sovellukseen paremmin sopivilla lisääntymisrutiineilla.