Pekka Orponen* and
Frédéric Prost**
* Department of Computer Science
University of Helsinki
P. O. Box 26, FIN-00014 Helsinki, Finland
E-mail: orponen@cs.helsinki.fi
** Département de Mathématiques et d'Informatique
Ecole Normale Supérieure de Lyon
69364 Lyon cedex 07, France
E-mail: fprost@lip.ens-lyon.fr
We describe a simple general purpose condition-action type parallel programming language and its implementation on Hopfield-type neural networks. A prototype compiler performing the translation has been implemented.
A PostScript version of this paper is available also at
http://www.cs.helsinki.fi/~orponen/papers/hopprog.ps
Keywords: neural networks , Hopfield nets , parallel programming
In addition to their uses in specific applications such as pattern classification, associative memory or combinatorial optimization recurrent neural networks are also theoretically universal, i.e., general-purpose computing devices. It was observed in [7] that sequences of polynomial-size recurrent threshold logic networks are computationally equivalent to (nonuniform) polynomial space-bounded Turing machines, and in [11] this equivalence was extended to polynomial-size sequences of networks with symmetric weights, i.e., ``Hopfield nets'' with hidden units. A corollary to the latter construction shows also that polynomial-size symmetric networks with small (i.e., polynomially bounded) interconnection weights are equivalent to polynomial time-bounded Turing machines. In [17] similar characterizations are proved concerning the computational power of asymmetric bounded-size networks with real-valued units and a saturated-linear transfer function. (All the networks discussed here and below have discrete synchronous dynamics, i.e., the states of all the units are updated in parallel discrete steps. However, see [12] for a simulation of synchronous Hopfield nets by totally asynchronous ones.)
An obvious next step after establishing such a universality result is to design a high-level programming language and a compiler appropriate for the model. For the analog asymmetric network model of [17] this was done in [16]; here we describe our approach to high-level programming of standard discrete symmetric Hopfield nets. Although the idea of high-level programming of neural nets may seem counterintuitive at first, we believe that methods for doing this will eventually be quite useful, considering the rapid progress in neural network hardware (see, for instance, the work presented in the compendium [15]).
A direct approach to the compilation would have been to simply implement
the Turing machine simulation scheme from [11].
This would, however, have been a waste
of the networks' capabilities, as this simulation forces the potentially
highly parallel network to behave in a purely sequential manner. Thus we
chose rather to experiment with a very simple parallel language,
where a program consists of a set of ``condition ![]() action'' pairs, to be executed repeatedly in parallel until
a ``halt''-action is encountered. The only operations performed
by our programs are elementary arithmetic and left and right shifts
on fixed-length integers, and the only conditions allowed are
conjunctions and disjunctions of numerical comparisons. The language
should obviously be enriched considerably to be of any practical use;
nevertheless even this prototype version is computationally universal
(within the limits set by the chosen integer length), and suffices to
try out the basic compilation principles.
action'' pairs, to be executed repeatedly in parallel until
a ``halt''-action is encountered. The only operations performed
by our programs are elementary arithmetic and left and right shifts
on fixed-length integers, and the only conditions allowed are
conjunctions and disjunctions of numerical comparisons. The language
should obviously be enriched considerably to be of any practical use;
nevertheless even this prototype version is computationally universal
(within the limits set by the chosen integer length), and suffices to
try out the basic compilation principles.
Finally, a few words on the broader motivation of this work. While the idea of high-level programming of neural nets may seem counterintuitive (after all, these are supposedly learning devices), there are at least two good reasons to consider the topic. Firstly, learning of concepts with high-level structure purely from raw data is very difficult (see, e.g. [6]), and thus it might be useful to have a method for initializing a network with an approximate solution, and use learning only for the fine-tuning of its parameters. Secondly, work on hardware implementations of neural network models progresses rapidly (see, for instance, the compendium [15]), and eventually ideas about high-level progamming methods for them will be very useful. (We might note that these motivations underlie, at least partly, also the by now quite large literature on neural representation of symbolic knowledge and ``hybrid'' neural-symbolic models; see, e.g. [4, 8, 9, 10, 14, 18].)
The compilation of programs from our simple parallel language into Hopfield networks proceeds in two stages: first the program is represented as a recurrent threshold logic network with asymmetric interconnections, and then this asymmetric network is ``symmetrized'' using the construction from [11]. Here we shall first describe the mapping into asymmetric networks, and then briefly the symmetrization procedure.
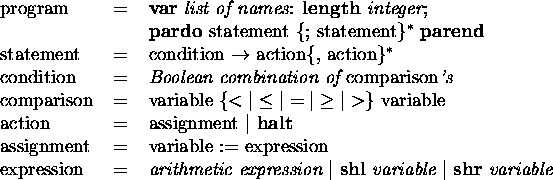
Figure: Syntax of a simple parallel language.
The syntax of our simple language is as described in Figure  .
As an elementary translation example, let us consider the following program
with two 8-bit integer variables x and y. Starting from any pair of
nonnegative initial values (satisfying the appropriate length constraints),
the program simply adjusts the values of the variables until they are equal,
and then halts.
.
As an elementary translation example, let us consider the following program
with two 8-bit integer variables x and y. Starting from any pair of
nonnegative initial values (satisfying the appropriate length constraints),
the program simply adjusts the values of the variables until they are equal,
and then halts.
var x, y: length 8;pardo
x < y
x := x+y, y := y-1;
x > y
x := x-y;
x = y
halt
parend.
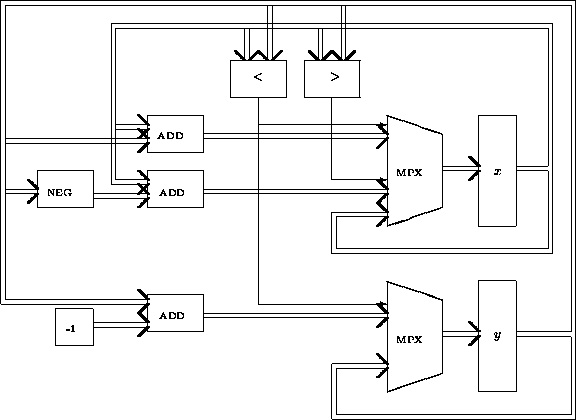
Figure: Asymmetric net corresponding to example program.
Schematically, this program would first be translated into the
asymmetric recurrent network shown in Figure  .
The boxes labeled x and y represent the 8-bit variable
registers, whose contents are first initialized with the input
values of the variables, and then repeatedly updated until a halting-test
module (not shown) determines that the values are equal and forces the
network to converge. The thick lines in Figure
.
The boxes labeled x and y represent the 8-bit variable
registers, whose contents are first initialized with the input
values of the variables, and then repeatedly updated until a halting-test
module (not shown) determines that the values are equal and forces the
network to converge. The thick lines in Figure  correspond
to 8-bit data lines around the network, and the thin lines to
single-bit controls. Note that all the possible assignments
for each variable are computed in parallel on each pass of data around
the network, and only at the end of the pass the control lines are used
to select the correct assignment, within a simple multiplexer
(MPX) subcircuit. In case none of the selector lines
are active, a multiplexer implicitly selects the old value
of the variable (the bottom input lines to the x and y multiplexers
in Figure
correspond
to 8-bit data lines around the network, and the thin lines to
single-bit controls. Note that all the possible assignments
for each variable are computed in parallel on each pass of data around
the network, and only at the end of the pass the control lines are used
to select the correct assignment, within a simple multiplexer
(MPX) subcircuit. In case none of the selector lines
are active, a multiplexer implicitly selects the old value
of the variable (the bottom input lines to the x and y multiplexers
in Figure  ). If many of the selector lines are active
simultaneously, the result of the multiplexing is undetermined.
). If many of the selector lines are active
simultaneously, the result of the multiplexing is undetermined.
In addition to the registers and the comparison and multiplexer modules,
Figure  shows three 8-bit adders (ADD),
one module (NEG) for transforming an 8-bit number into
its negative in a two's complement representation, and one
constant input module (-1).
All these subcircuits are quite easy to build using threshold logic
units: for instance the comparisons require just one unit each, and
each multiplexer consists of 8 two-way one-bit selectors, each of size 3,
plus the additional circuitry needed to implement the default selection.
The most complicated modules are the adders, whose implementation
we moreover have not even attempted to optimize. For an 8-bit
adder we simply chain together 8 single-bit full adders. (This is
perhaps the main aspect of our compiler that needs improvement.
The current design is bad not only because it consumes a lot of units,
but also because it introduces long delays into the network and complicates
its sequencing.) In addition to the modules shown in the figure,
the network also contains a certain amount of control circuitry,
e.g. for implementing the halt operation, and ensuring that
all the inputs required by a module arrive at the same time.
shows three 8-bit adders (ADD),
one module (NEG) for transforming an 8-bit number into
its negative in a two's complement representation, and one
constant input module (-1).
All these subcircuits are quite easy to build using threshold logic
units: for instance the comparisons require just one unit each, and
each multiplexer consists of 8 two-way one-bit selectors, each of size 3,
plus the additional circuitry needed to implement the default selection.
The most complicated modules are the adders, whose implementation
we moreover have not even attempted to optimize. For an 8-bit
adder we simply chain together 8 single-bit full adders. (This is
perhaps the main aspect of our compiler that needs improvement.
The current design is bad not only because it consumes a lot of units,
but also because it introduces long delays into the network and complicates
its sequencing.) In addition to the modules shown in the figure,
the network also contains a certain amount of control circuitry,
e.g. for implementing the halt operation, and ensuring that
all the inputs required by a module arrive at the same time.
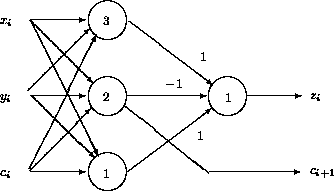
Figure: A single-bit full adder subcircuit.
As an example of threshold logic design, Figure  shows a full adder that adds bits
shows a full adder that adds bits ![]() ,
, ![]() , and
, and ![]() , to produce
output bit
, to produce
output bit ![]() and carry bit
and carry bit ![]() . All the weights in the
first layer of the circuit are 1.
. All the weights in the
first layer of the circuit are 1.
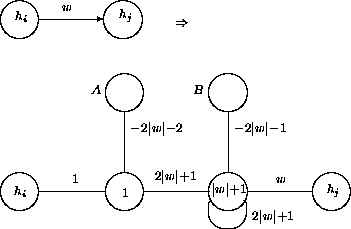
Figure: A sequence of symmetric edges corresponding to an asymmetric
edge of weight w.
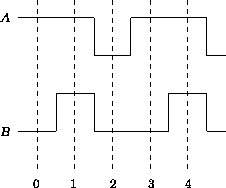
Figure: The clock pulse sequence used in the edge simulation.
The procedure for transforming convergent asymmetric nets into symmetric
ones is discussed in detail in [11]; here we provide only an
outline. In the transformation, each asymmetric edge in the original
network is first replaced by a sequence of three symmetric edges and their
intermediate units, as indicated in Figure  . The two
intermediate units act like locks in a canal, permitting information
to flow only from left to right. The locks are sequenced by clock pulses
emanating from the units labeled A and B, in cycles of period three
as presented in Figure
. The two
intermediate units act like locks in a canal, permitting information
to flow only from left to right. The locks are sequenced by clock pulses
emanating from the units labeled A and B, in cycles of period three
as presented in Figure  . (This edge simulation technique
was originally introduced, in a somewhat more complicated form, by Hartley
and Szu in [3].)
. (This edge simulation technique
was originally introduced, in a somewhat more complicated form, by Hartley
and Szu in [3].)
Figure: A three-bit binary counter network.
Because symmetric nets always converge to either a stable state or
a cycle of period two [2], a proper clock of period three
cannot actually be constructed in a symmetric net. However, to simulate
a convergent computation of the original asymmetric net,
it suffices to have a clock that produces an exponential number
of periods and then stops. (Note that a convergent synchronous computation
on n units must terminate within ![]() steps, because otherwise the
network repeats a configuration and goes into a cycle.) Such a clock
can be obtained from, e.g., a symmetric exponential-transient network
designed by Goles and Martínez [1].
The first two stages in the construction of this network are
presented in Figure
steps, because otherwise the
network repeats a configuration and goes into a cycle.) Such a clock
can be obtained from, e.g., a symmetric exponential-transient network
designed by Goles and Martínez [1].
The first two stages in the construction of this network are
presented in Figure  .
.
The idea here is that the n units in the upper row implement a binary counter, counting from all 0's to all 1's (in the figure, the unit corresponding to the least significant bit is to the right). For each ``counter'' unit added to the upper row, after the two initial ones, two ``control'' units are added to the lower row. The purpose of the latter is to first turn off all the ``old'' units, when the new counter unit is activated, and from then on balance the input coming to the old units from the new units, so that the old units may resume counting from zero.
The required period-three clock may now be obtained from the second counter unit of this network by means of an appropriate delay line construction. In building this connection, the weights and the thresholds in the counter network must also be multiplied by some sufficiently large constant so that the rest of the network has no effect back on the clock. For more details of the construction, see [11].
We have designed and implemented an experimental compiler from a very simple condition-action type parallel programming language into standard symmetric discrete Hopfield networks with synchronous dynamics. The programming language should be extended considerably to be practical, and some of the design decisions in the compiler (notably the simplistic implementation of arithmetic modules) have turned out to be less than optimal. Nevertheless, this is to our knowledge the first attempt at general-purpose high-level programming on this standard and theoretically well-studied computational model.
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.