

Next: The algorithm
Up: Independent Component Analysis
Previous: Independent Component Analysis
In blind source separation, the original independent sources are
assumed to be unknown, and we only have access to their weighted sum.
In this model, the signals recorded in an MEG study are noted as
xk(i) (i ranging from 1 to L, the number of sensors used,
and k denoting discrete time); see Fig. ![[*]](cross_ref_motif.gif) . Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
. Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
| 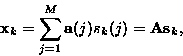 |
(1) |
where ![${\bf x}_k = [x_k(1), \dots, x_k(L)]^T$](img4.gif) is an L-dimensional
data vector, made up of the L mixtures at discrete time k. The
is an L-dimensional
data vector, made up of the L mixtures at discrete time k. The
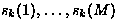 are the
M zero mean independent source signals, and
are the
M zero mean independent source signals, and ![${\bf A} = [{\bf a}(1),
\dots, {\bf a}(M)]$](img6.gif) is a mixing matrix independent of time whose elements
aij are the unknown coefficients of the mixtures. In order to
perform ICA, it is necessary to have at least as many mixtures as
there are independent sources (
is a mixing matrix independent of time whose elements
aij are the unknown coefficients of the mixtures. In order to
perform ICA, it is necessary to have at least as many mixtures as
there are independent sources (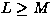 ). When this relation is not
fully guaranteed, and the dimensionality of the problem is high enough,
we should expect the first independent components to present clearly
the most strongly independent signals, while the last components still
consist of mixtures of the remaining signals. In our
study, we did expect that the artifacts, being
clearly independent from the brain activity, should come out in the
first independent components. The remaining of the brain activity
(e.g.
). When this relation is not
fully guaranteed, and the dimensionality of the problem is high enough,
we should expect the first independent components to present clearly
the most strongly independent signals, while the last components still
consist of mixtures of the remaining signals. In our
study, we did expect that the artifacts, being
clearly independent from the brain activity, should come out in the
first independent components. The remaining of the brain activity
(e.g. 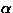 and
and 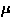 rhythms) may need some further processing.
rhythms) may need some further processing.
The mixing matrix 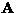 is a function of the geometry of the
sources and the electrical conductivities of the brain,
cerebrospinal fluid, skull and scalp. Although this matrix is
unknown, we assume it to be constant, or slowly changing (to preserve
some local constancy).
is a function of the geometry of the
sources and the electrical conductivities of the brain,
cerebrospinal fluid, skull and scalp. Although this matrix is
unknown, we assume it to be constant, or slowly changing (to preserve
some local constancy).
The problem is now to estimate the independent signals sk (j) from
their mixtures, or the equivalent problem of finding the separating
matrix 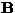 that satisfies (see Eq.
that satisfies (see Eq. ![[*]](cross_ref_motif.gif) )
)
| 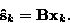 |
(2) |
In our algorithm, the solution uses the statistical definition of
fourth-order cumulant or kurtosis that, for the ith source
signal, is defined as
![\begin{displaymath}
kurt(s(i)) = E\{s(i)^4\} - 3[E\{s(i)^2\}]^2,\end{displaymath}](img13.gif)
where E(s) denotes the mathematical expectation of s.


Next: The algorithm
Up: Independent Component Analysis
Previous: Independent Component Analysis
Ricardo Vigario
3/3/1998
![[*]](cross_ref_motif.gif) . Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
. Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
![[*]](cross_ref_motif.gif) . Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
. Each
xk(i) is expressed as the weighted sum of M independent signals
sk(j), following the vector expression:
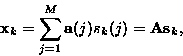
![]() is a function of the geometry of the
sources and the electrical conductivities of the brain,
cerebrospinal fluid, skull and scalp. Although this matrix is
unknown, we assume it to be constant, or slowly changing (to preserve
some local constancy).
is a function of the geometry of the
sources and the electrical conductivities of the brain,
cerebrospinal fluid, skull and scalp. Although this matrix is
unknown, we assume it to be constant, or slowly changing (to preserve
some local constancy).
![]() that satisfies (see Eq.
that satisfies (see Eq. ![[*]](cross_ref_motif.gif) )
)
![]()