



Next: Control
Up: Nonlinear state-space models
Previous: Nonlinear state-space models
Contents
In linear state space models, the sequence of states or sources
 can be exactly inferred from data with an algorithm
called the Kalman smoothing by Kalman (1960) (see also Anderson and Moore, 1979).
Ghahramani and Beal (2001) show how belief propagation and the junction
tree algorithms can be used in the inference in the variational
Bayesian setting. As an example they perform inference in linear
state-space models. Exact inference is accomplished using a single
forward and backward sweep. Unfortunately these results do not apply to
nonlinear state space models.
can be exactly inferred from data with an algorithm
called the Kalman smoothing by Kalman (1960) (see also Anderson and Moore, 1979).
Ghahramani and Beal (2001) show how belief propagation and the junction
tree algorithms can be used in the inference in the variational
Bayesian setting. As an example they perform inference in linear
state-space models. Exact inference is accomplished using a single
forward and backward sweep. Unfortunately these results do not apply to
nonlinear state space models.
The idea behind iterated extended Kalman smoother
(see Anderson and Moore, 1979) is to linearise the mappings
 and
and
 around the current state estimates
around the current state estimates
 using the first terms of the Taylor
series expansion. The algorithm alternates between updating the states
by Kalman smoothing and renewing the linearisation. When
the system is highly nonlinear or the initial estimate is poor, the
iterated extended Kalman smoother may diverge.
The iterative unscented Kalman smoother by Julier and Uhlmann (1997) replaces the
local linearisation by a deterministic sampling technique. The
sampled points are propagated through the nonlinearities, and a Gaussian
distribution is fitted to them. The use of
non-local information improves convergence and accuracy at the cost of
doubling the computational complexity, but still there
is no guarantee of convergence.
using the first terms of the Taylor
series expansion. The algorithm alternates between updating the states
by Kalman smoothing and renewing the linearisation. When
the system is highly nonlinear or the initial estimate is poor, the
iterated extended Kalman smoother may diverge.
The iterative unscented Kalman smoother by Julier and Uhlmann (1997) replaces the
local linearisation by a deterministic sampling technique. The
sampled points are propagated through the nonlinearities, and a Gaussian
distribution is fitted to them. The use of
non-local information improves convergence and accuracy at the cost of
doubling the computational complexity, but still there
is no guarantee of convergence.
Particle filtering (Doucet et al., 2001) is an increasingly popular method
for state inference. It generates random samples from the posterior
distribution. The basic version requires a large number of particles
or samples to provide a reasonable accuracy. If the state space is
high dimensional, the sufficient number of samples can become
prohibitively large. There are many improvements for the basic
algorithm to improve efficiency. One of them, Rao-Blackwellisation
(see e.g. Ristic et al., 2004), uses analytical solutions to some of the
filtering equations instead of pure sampling.
Variational Bayesian inference in nonlinear state-space models is
based on updating the posterior approximation of states for minimising
the cost function
 . Recall that
. Recall that
 is a sum of simple
terms. Terms that involve a certain state
is a sum of simple
terms. Terms that involve a certain state
 at time
at time  are
independent of all the other states except the closest neighbours
are
independent of all the other states except the closest neighbours
 and
and
 . Most optimisation algorithms would thus
only consider information from the closest neighbours for each update.
Information spreads around slowly because the states of different time
slices affect each other only between updates. It is possible to
predict this interaction by a suitable approximation.
. Most optimisation algorithms would thus
only consider information from the closest neighbours for each update.
Information spreads around slowly because the states of different time
slices affect each other only between updates. It is possible to
predict this interaction by a suitable approximation.
Publication V introduces an update
algorithm for the posterior mean of the states
 by
approximating total derivatives
by
approximating total derivatives
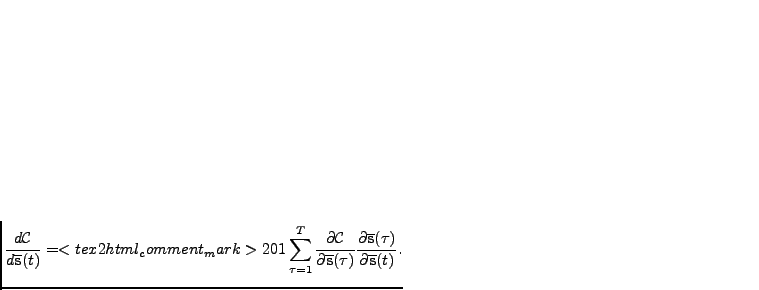 |
(4.12) |
Once we can approximate
 and
and
 by linearising the
mappings
by linearising the
mappings
 and
and
 , the total derivatives are computed
efficiently using the chain rule and dynamic programming. To
summarise, the novel algorithm is based on minimising a variational
Bayesian cost function and the novelty is in propagating the gradient
, the total derivatives are computed
efficiently using the chain rule and dynamic programming. To
summarise, the novel algorithm is based on minimising a variational
Bayesian cost function and the novelty is in propagating the gradient
 through the state
sequence.
through the state
sequence.
When an algorithm is based on minimising a cost function, it is fairly
easy to guarantee convergence. While the Kalman filter is clearly the
best choice for inference in linear Gaussian models, the problem with
many of the nonlinear generalisation is that they cannot guarantee
convergence. Even when the algorithms converge, convergence can be
slow. Another recent fix for convergence by Psiaki (2005) comes
with a large computational cost.
Publication V compares the proposed algorithm to
some of the existing methods using two experimental setups: Simulated
double inverted pendulum and real-world speech spectra. The results
were better than any of the comparison methods in all cases. The
comparison to particle filtering was not conclusive because the
particle filter was not Rao-Blackwellisised.




Next: Control
Up: Nonlinear state-space models
Previous: Nonlinear state-space models
Contents
Tapani Raiko
2006-11-21
 can be exactly inferred from data with an algorithm
called the Kalman smoothing by Kalman (1960) (see also Anderson and Moore, 1979).
Ghahramani and Beal (2001) show how belief propagation and the junction
tree algorithms can be used in the inference in the variational
Bayesian setting. As an example they perform inference in linear
state-space models. Exact inference is accomplished using a single
forward and backward sweep. Unfortunately these results do not apply to
nonlinear state space models.
can be exactly inferred from data with an algorithm
called the Kalman smoothing by Kalman (1960) (see also Anderson and Moore, 1979).
Ghahramani and Beal (2001) show how belief propagation and the junction
tree algorithms can be used in the inference in the variational
Bayesian setting. As an example they perform inference in linear
state-space models. Exact inference is accomplished using a single
forward and backward sweep. Unfortunately these results do not apply to
nonlinear state space models.
 and
and
 around the current state estimates
around the current state estimates
 using the first terms of the Taylor
series expansion. The algorithm alternates between updating the states
by Kalman smoothing and renewing the linearisation. When
the system is highly nonlinear or the initial estimate is poor, the
iterated extended Kalman smoother may diverge.
The iterative unscented Kalman smoother by
using the first terms of the Taylor
series expansion. The algorithm alternates between updating the states
by Kalman smoothing and renewing the linearisation. When
the system is highly nonlinear or the initial estimate is poor, the
iterated extended Kalman smoother may diverge.
The iterative unscented Kalman smoother by  . Recall that
. Recall that
 at time
at time  are
independent of all the other states except the closest neighbours
are
independent of all the other states except the closest neighbours
 and
and
 . Most optimisation algorithms would thus
only consider information from the closest neighbours for each update.
Information spreads around slowly because the states of different time
slices affect each other only between updates. It is possible to
predict this interaction by a suitable approximation.
. Most optimisation algorithms would thus
only consider information from the closest neighbours for each update.
Information spreads around slowly because the states of different time
slices affect each other only between updates. It is possible to
predict this interaction by a suitable approximation.
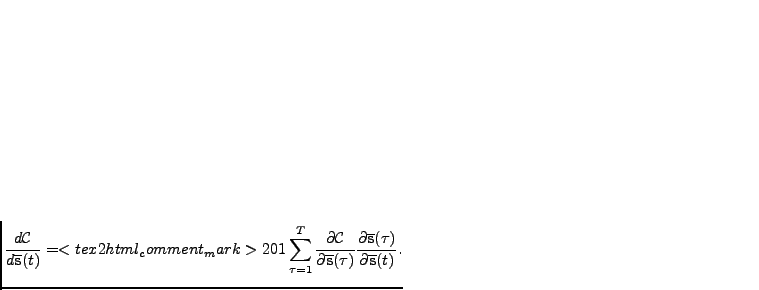
 and
and
 by linearising the
mappings
by linearising the
mappings
 through the state
sequence.
through the state
sequence.