 through a square
mixing matrix
through a square
mixing matrix
 by
by
The mixing model of independent component analysis (ICA) is similar to
that of the FA (see Figure 3.2), but in the basic case with equal
number of factors (or components) as observations and without the noise term. The
data is thought to have been generated from independent components
 through a square
mixing matrix
through a square
mixing matrix
 by
by
 are independent, that is,
are independent, that is,
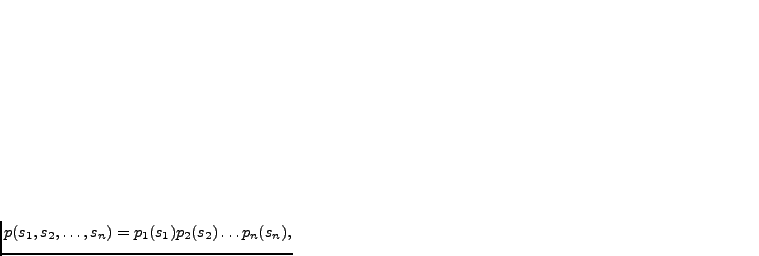 |
(3.19) |
In the basic case, the number of components is the same as the number
of observation and the components can be reconstructed from data given
the mixing matrix
 by
by
 .
The independence of the reconstructed
.
The independence of the reconstructed
 can then be measured for
instance by the non-Gaussianity of the components or by
mutual information (Hyvärinen et al., 2001). ICA can thus be done by iteratively maximising such a measure.
ICA has many fields of applications, such as brain imaging
(Vigário et al., 1998), telecommunications
(Raju et al., 2006; Ristaniemi, 2000), speech separation, and so on (Hyvärinen et al., 2001).
can then be measured for
instance by the non-Gaussianity of the components or by
mutual information (Hyvärinen et al., 2001). ICA can thus be done by iteratively maximising such a measure.
ICA has many fields of applications, such as brain imaging
(Vigário et al., 1998), telecommunications
(Raju et al., 2006; Ristaniemi, 2000), speech separation, and so on (Hyvärinen et al., 2001).
ICA can be approached from different starting points. It can be viewed as a Bayesian network when the one dimensional distributions for the components are modelled with for example mixtures-of-Gaussians (Miskin and MacKay, 2001; Attias, 2001,1999; Choudrey et al., 2000). This is also known as independent factor analysis. Extensions to the basic ICA involve additive noise, convolutive or nonlinear mixing, and the number of components might differ from the number of observations (Hyvärinen et al., 2001).
Publication III studies the reconstruction of corrupted values in data by independent factor analysis.