 , burglary by
, burglary by  and so on, the joint probability can be factored
into
and so on, the joint probability can be factored
into
Let us study an example by Pearl (1988). Mr. Holmes receives a
phone call from his neighbour about an alarm in his house. As he is
debating whether or not to rush home, he remembers that the alarm
might have been triggered by an earthquake. If an earthquake had
occurred, it might be on the news, so he turns on his radio. The events
are shown in Figure 3.1. Marking the events earthquake by
 , burglary by
, burglary by  and so on, the joint probability can be factored
into
and so on, the joint probability can be factored
into
 does not
depend on whether there is a burglary
does not
depend on whether there is a burglary  or not, given that we know
whether there was an earthquake or not, so
or not, given that we know
whether there was an earthquake or not, so
 .
.
![\includegraphics[width=0.97\textwidth]{alarm.eps}](img103.png)
|
The graphical representation of the conditional probabilities depicted
in the top left subfigure of Figure 3.1 is intuitive:
arrows point from causes to effects. Note that the graph has to be
acyclic, no occurrence can be its own cause. Loops, or cycles when
disregarding directions of the edges, are allowed. Assuming that the
variables are discrete, the conditional probabilities are described
using a conditional probability table that lists probabilities for all
combinations of values for the relevant variables. For instance,
 is described in Table 3.1.
Recalling the notation from Section 2.3, the
numbers in the conditional probability table are parameters
is described in Table 3.1.
Recalling the notation from Section 2.3, the
numbers in the conditional probability table are parameters
 while unobserved variables in the nodes are
while unobserved variables in the nodes are
 .
.
Inference in Bayesian networks solves questions such as ``what is the probability of burglary given that neighbour 1 calls about the alarm?'' Approximate inference methods such as sampling (see Section 2.5.4) can be used, but in relatively simple cases, also exact inference can be done. For that purpose, we will form the join tree of the Bayesian network. First, we connect parents of a node to each other, and remove all directions of the edges, (see top right subfigure of Figure 3.1). This is called a Markov network. Next, we find all cliques (fully connected subgraphs) of the Markov network. Then we create a join tree3.1 where nodes represent the cliques in the Markov network and edges are set between nodes who share some variables (see bottom subfigure of Figure 3.1).
We can rewrite the joint distribution in Equation 3.1 as
 and marginalising the
uninteresting variables away:
and marginalising the
uninteresting variables away:
 true true |
 |
|
 true true |
||
 true true |
||
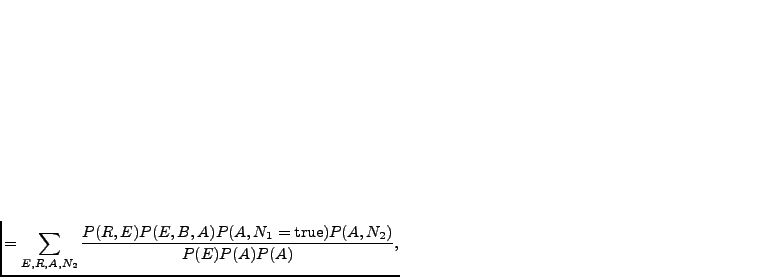 |
(3.2) |
 means ``proportional to''. The constant
means ``proportional to''. The constant
 true
true can be ignored if the resulting distribution is
normalised in the end. Summing over all the latent variables is often
prohibitively computationally expensive, so better means have been
found.
can be ignored if the resulting distribution is
normalised in the end. Summing over all the latent variables is often
prohibitively computationally expensive, so better means have been
found.
For efficient marginalisation in join trees, there is an algorithm
called belief propagation (Pearl, 1988) based on message
passing. First, any one of the nodes in the join tree is selected as a
root. Messages  are sent away from the root and messages
are sent away from the root and messages
 towards the root. The marginal posterior probability of a node
towards the root. The marginal posterior probability of a node
 in the join tree given observations
in the join tree given observations  is decomposed into two parts:
is decomposed into two parts:
 |
 anc(X) anc(X) desc(X) desc(X) |
|
 |
(3.3) |
 anc(X) and
anc(X) and
 desc(X) are the
observations in the ancestor and descendant nodes of
desc(X) are the
observations in the ancestor and descendant nodes of  in the join
tree accordingly. The messages can be computed recursively by
in the join
tree accordingly. The messages can be computed recursively by
 |
 |
(3.4) |
 |
 |
(3.5) |
 |
 |
(3.6) |
 is the parent of
is the parent of  in the join tree and
in the join tree and  are its
children, including
are its
children, including  . The message
. The message  for the root node is set to
the prior probability of the node, and the messages
for the root node is set to
the prior probability of the node, and the messages  are set
to uniform distribution for the unobserved leaf nodes.
The belief propagation algorithm extended for logical hidden Markov models in Publication VII.
are set
to uniform distribution for the unobserved leaf nodes.
The belief propagation algorithm extended for logical hidden Markov models in Publication VII.
Returning to the example in Equation 3.2 and
selecting node  as the root of the join tree, the necessary
messages are
as the root of the join tree, the necessary
messages are
 |
 |
(3.7) |
 |
 |
(3.8) |
 |
 |
(3.9) |
 |
 |
(3.10) |
 and
and
 are uniform (unobserved leaf
nodes), it is easy to see that
are uniform (unobserved leaf
nodes), it is easy to see that
 and
and
 are also uniform and can thus be ignored. We get
are also uniform and can thus be ignored. We get
 true true |
 |
|
 |
||
 true true |
||
 true true |
(3.11) |
For the inference to be exact, the join tree must not have loops (like the name implies). Loopy belief propagation by Murphy et al. (1999) uses belief propagation algorithm regardless of loops. Experiments show that in many cases it still works fine. The messages are initialised uniformly and iteratively updated until the process hopefully converges. It is also possible to find an exact solution by getting rid of loops at the cost of increased computational complexity. This happens by adding edges to the Markov network.
Bayesian networks can manage continuous valued variables, when three simplifying assumptions are made (Pearl, 1988). All interactions between variables are linear, the sources of uncertainty are normally distributed, and the causal network is singly connected (no two nodes share both common descendants and common ancestors). Instead of tables, the conditional probabilities are described with linear mappings. Posterior probability is Gaussian.
Bayesian networks are static, that is, each data sample is independent
from others. The extension to dynamic (or temporal) Bayesian networks
(see Ghahramani, 1998) is straightforward. Assume that
the data samples
 , e.g.
, e.g.
 , are indexed by time
, are indexed by time  . Each variable can have as
parents variables of sample
. Each variable can have as
parents variables of sample
 in addition to the variables of
the sample itself
in addition to the variables of
the sample itself
 . Hidden Markov models (see Section 3.1.5) are an
important special case of dynamic Bayesian networks.
. Hidden Markov models (see Section 3.1.5) are an
important special case of dynamic Bayesian networks.
Linearity assumption can be relaxed when some approximations are made. Section 4.4 and Publication I present such a framework based on variational Bayesian learning. There are also other approaches. Hofmann and Tresp (1996) study Bayesian networks with nonlinear conditional density estimators. Inference is based on Gibbs sampling and learning is based on cross-validated maximum a posteriori estimation.