Introduction

Growing amount of data is collected every day in all fields of life. For the purpose of automatic analysis, prediction, denoising, classification etc. of data, a huge number of models have been created. It is natural that a specific model for a specific purpose works often the best, but still, a general method to handle any kind of data would be very useful. For instance, if an artificial brain has a large number of completely separate modules for different tasks, the interaction between the modules becomes difficult. Probabilistic modelling provides a well-grounded framework for data analysis. This paper describes a probabilistic model that can handle data with relations as well as discrete and continuous values with nonlinear dependencies.

Terminology: Using Prolog notation, we write $\mathrm{knows}(\mathrm{alex},\mathrm{bob})$ for stating a fact that the $\mathrm{knows}$ relation holds between the objects $\mathrm{alex}$ and $\mathrm{bob}$, that is, Alex knows Bob. The arity of the relation tells how many objects are involved. The $\mathrm{knows}$ relation is binary, that is, between two objects, but in general relations can be of any arity. The atom $\mathrm{knows}(\mathrm{alex},B)$ matches all the instances where the variable $B$ represents an object known by Alex. In this paper, the terms are restricted to constants and variables, that is, compound terms such as $\mathrm{thinks}(A,\mathrm{knows}(B,A))$ are not considered. For every relation that is logically true, there are associated attributes ${\mathbf{x}}$, say a class label or a vector of real numbers. The attributes ${\mathbf{x}}(\mathrm{knows}(A,B))$ describe how well $A$ knows $B$ and whether $A$ likes or dislikes $B$. The attribute vector ${\mathbf{x}}(\mathrm{con}(A))$ describes what kind of a consumer the person $A$ is. Given a relational database describing relationships between people and their consuming habits, we might study the dependencies that might be found. For instance, some people cloth like their idols, and nonsmokers tend to be friends with nonsmokers. The modelling can be done for instance by finding all occurrences of the template $(\mathrm{con}(A), \mathrm{knows}(A,B), \mathrm{con}(B))$ in the data and studying the distribution of the corresponding attributes. The situation is depicted in Figure 1.

Figure: Consider a relational database describing the relationships and consumer habits of three people. The two tables are shown on the left. On the right, the database is represented graphically, with the occurrences of the template $(\mathrm{con}(A), \mathrm{knows}(A,B), \mathrm{con}(B))$ marked with ovals on the very right.

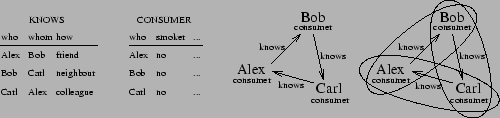Bayesian networks[6] are popular statistical models based on a directed graph. The graph has to be acyclic, which is in line with the idea that the arrows represent causality: an occurrence cannot be its own cause. In relational generalisations of Bayesian networks [7], the graphical structure is determined by the data. Often it can be assumed that the data does not contain cycles, for instance in the case when the direction of the arrows is always from the past to the future. Sometimes the data has cycles, like in Figure 1. Markov networks [6], on the other hand, are based on undirected graphical models. A Markov network does not care whether $A$ caused $B$ or vice versa, it is interested only whether there is a dependency or not.