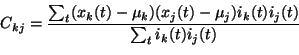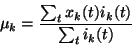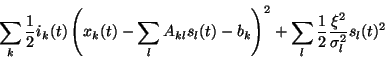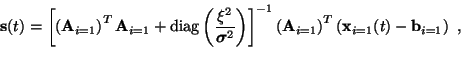


Next: Experiments
Up: Linear and Nonlinear Factor
Previous: The Missing Values
The posterior variances of the factors are initialised to small
values, but a simple linear method is applied to find sensible
posterior means of the factors. The model is similar to the FA model
given by (3 - 5) with the exception that the
variance of the noise is constant
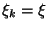 for each dimension
k.
In principal component analysis (PCA) the matrix
A is formed
from the eigenvectors of the covariance matrix
C of the data.
The eigenvectors corresponding to the largest eigenvalues are chosen,
since the eigenvalues are the variances
for each dimension
k.
In principal component analysis (PCA) the matrix
A is formed
from the eigenvectors of the covariance matrix
C of the data.
The eigenvectors corresponding to the largest eigenvalues are chosen,
since the eigenvalues are the variances
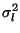 which should
be maximised. In this case,
C is calculated from only those
pairs of data values where both values are observed:
which should
be maximised. In this case,
C is calculated from only those
pairs of data values where both values are observed:
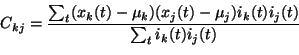 |
(9) |
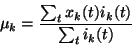 |
(10) |
The maximum a posteriori estimate for
s which is also the mean of the posterior distribution, is found by minimising
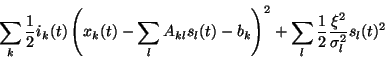 |
(11) |
and the solution is
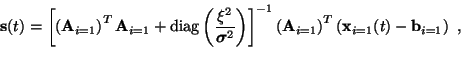 |
(12) |
where subscript i=1 stands for using only those rows or
dimensions, where the corresponding dimension of
i(t) is
one.
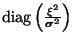 stands for
a diagonal square matrix, whose diagonal values are
stands for
a diagonal square matrix, whose diagonal values are
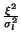 .
The noise variance
.
The noise variance 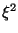 is left as
a parameter.
is left as
a parameter.
The initialisation values of the factors are important, because they
are fixed for the first 50 sweeps through the entire data set. This
allows the network to find a meaningful mapping from factors to the
observations, thereby justifying using the factors for the
representation. For the same reason, the parameters controlling the
distributions of the factors, weights, noise and the hyperparameters
are not adapted during the first 100 sweeps. They are adapted only
after the network has found sensible values for the variables whose
distributions these parameters control. This setting is important for
the method because the network can effectively prune away unused
parts, which would lead to a local minimum from which the network
would never recover.



Next: Experiments
Up: Linear and Nonlinear Factor
Previous: The Missing Values
Tapani Raiko
2001-09-26
![]() for each dimension
k.
In principal component analysis (PCA) the matrix
A is formed
from the eigenvectors of the covariance matrix
C of the data.
The eigenvectors corresponding to the largest eigenvalues are chosen,
since the eigenvalues are the variances
for each dimension
k.
In principal component analysis (PCA) the matrix
A is formed
from the eigenvectors of the covariance matrix
C of the data.
The eigenvectors corresponding to the largest eigenvalues are chosen,
since the eigenvalues are the variances
![]() which should
be maximised. In this case,
C is calculated from only those
pairs of data values where both values are observed:
which should
be maximised. In this case,
C is calculated from only those
pairs of data values where both values are observed: