

Next: 4. Experiments
Up: 1. The VQ model
Previous: 1. The VQ model
Minimization of Eq. 1 is carried out so that C is fixed
and the cost is minimized with respect to each of the variables
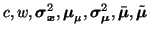 .
The following steps are repeated
iteratively as long as the value of the cost function decreases or
maximum iteration count is reached (in our experiments 100
iterations). This is repeated for various values of C.
.
The following steps are repeated
iteratively as long as the value of the cost function decreases or
maximum iteration count is reached (in our experiments 100
iterations). This is repeated for various values of C.
- 1.
- Winner selection.
- 2.
- Update of the winner.
- (a)
- Update of the posterior mean of the codebook vector.
- (b)
- Update of the posterior variance of the codebook vector.
- 3.
- Update of the data variance.
- 4.
- Updates of codebook frequency prior and parameters of the prior distribution.
Here f(i) is the number of hits of
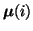 ,
i.e.,
,
i.e.,
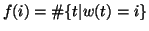 .
.
Krista Lagus
2001-08-28
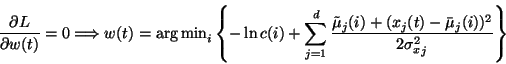
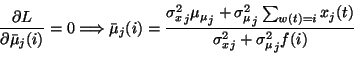
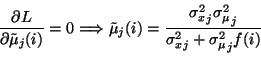
![\begin{displaymath}\frac{\partial L}{\partial {\sigma^2_x}_j} = 0 \Longrightarro...
... \tilde{\mu}_j(w(t)) + ( x_j(t)- \bar{\mu}_j(w(t)))^2 \right]
\end{displaymath}](img29.gif)
![\begin{displaymath}c(i) = \frac{f(i)+1}{N + C}, \hspace{3mm} {\mu_\mu}_j = \frac...
...=1}^C [\tilde{\mu}_j(i) + {(\bar{\mu}_j(i) - {\mu_\mu}_j)}^2]
\end{displaymath}](img30.gif)
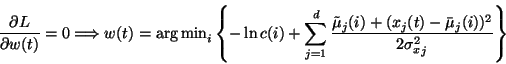
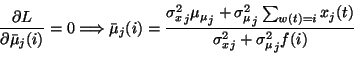
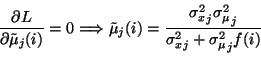
![\begin{displaymath}\frac{\partial L}{\partial {\sigma^2_x}_j} = 0 \Longrightarro...
... \tilde{\mu}_j(w(t)) + ( x_j(t)- \bar{\mu}_j(w(t)))^2 \right]
\end{displaymath}](img29.gif)
![\begin{displaymath}c(i) = \frac{f(i)+1}{N + C}, \hspace{3mm} {\mu_\mu}_j = \frac...
...=1}^C [\tilde{\mu}_j(i) + {(\bar{\mu}_j(i) - {\mu_\mu}_j)}^2]
\end{displaymath}](img30.gif)