To demonstrate the approach, we will describe
![]() where each
variable group is modeled using a different VQ. From now on, we will
refer to the cost function of a single variable group leaving out the
group index g.
where each
variable group is modeled using a different VQ. From now on, we will
refer to the cost function of a single variable group leaving out the
group index g.
The vector quantization model used for a single variable group
consists of codebook vectors
![]() (described
by their means and a common variance) and indices of the
winners w(t) for each data vector
(described
by their means and a common variance) and indices of the
winners w(t) for each data vector
![]() .
.
For finding
![]() we use variational EM-algorithm with
we use variational EM-algorithm with
![]() as missing observations. In the E-phase, an upper
bound of the cost is minimized [2,5]. The rest
of the parameters are included in H, i.e. we use ML estimates for
the following: c, the hyper parameter governing the prior
probability for a codebook vector to be a winner;
as missing observations. In the E-phase, an upper
bound of the cost is minimized [2,5]. The rest
of the parameters are included in H, i.e. we use ML estimates for
the following: c, the hyper parameter governing the prior
probability for a codebook vector to be a winner;
![]() ,
the diagonal
elements of the common covariance matrix; and
,
the diagonal
elements of the common covariance matrix; and
![]() and
and
![]() ,
the
hyper parameters governing the mean and variance of the prior
distribution of the codebook vectors.
,
the
hyper parameters governing the mean and variance of the prior
distribution of the codebook vectors.
The upper bound for
![]() is obtained from
is obtained from
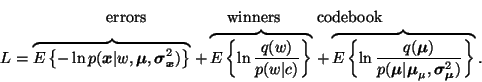
![[*]](foot_motif.gif)