2. Related models

  

Figure: Schematic illustrations of IVGA and related algorithms, namely MICA/ISA and FVQ that each look for multi-dimensional feature subspaces in effect by maximizing a statistical independency criterion. The input ${\bf x}$ is here 9-dimensional. The numbers of squares in FVQ and IVGA denote the numbers of variables modeled in each sub-model, and the numbers of black arrows in MICA the dimensionality of the subspaces.

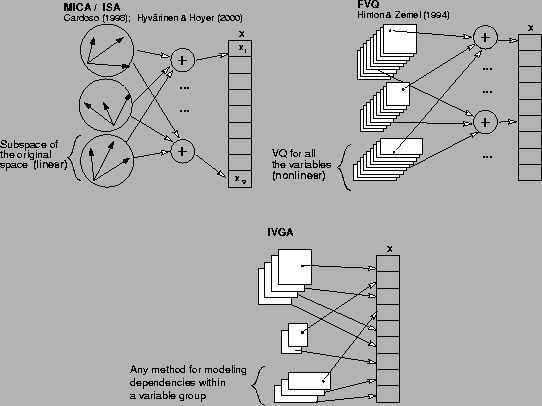
In multidimensional independent component analysis (MICA) [1], and its subsequent development independent subspace analysis (ISA) [4], the idea is to find independent linear feature subspaces that can be used to reconstruct the data efficiently. Thus each subspace is able to model the linear dependences in terms of the latent directions defining the subspace. The approach bears resemblance to IVGA which can be seen as a nonlinear version of MICA with the additional requirement which restricts the subspaces to be spanned by subsets of the variable axes.

Factorial vector quantization (FVQ) [3,7] can be seen as a nonlinear version of MICA. It uses several different VQs that cooperate to reconstruct the observations and is thus very similar to ${\rm IVGA_{VQ}}$. The structural differences of the FVQ model compared to the ${\rm IVGA_{VQ}}$ model are: in FVQ (1) each vector in each pool or group contains all the components (variables) of the original input vector, and (2) these are summed to produce the value of a single output. In contrast, in ${\rm IVGA_{VQ}}$ each variable group is modeled by exactly one vector quantizer (VQ). This leads to efficient computation as each VQ can operate independently as opposed to FVQ where the winners are found iteratively.

Figure 1 illustrates the model structures of MICA/ISA, FVQ, and IVGA.