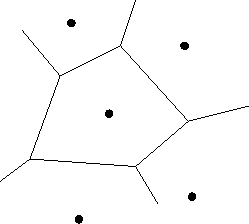
Figure 4.2: Voronoi tesselations in the input space
The SOM representation is a generalization of the underlying data [19]. It can be used as a basis for further processing. The SOM representation is a lattice of discrete points in the n-dimensional input space. The SOM can be used to partition the input data to smaller regions by associating input data with their best-matching units. Each data point in input space has, by definition, one best matching unit. The area in the input space for which the codebook vector is the BMU is called Voronoi tesselation. Voronoi tesselations partition the input space into disjoint sets.

Figure 4.2: Voronoi tesselations in the input space
A model can be created by fitting a model to the data in the Voronoi tesselation. By way of doing this, one can create models that are local to the specific Voronoi tesselation. These models desrcibe the behavior of the system in this local space only. One could also combine data coming from a neuron and its neighboring units to form a larger amount of data covering a larger amount of input space thus enlarging the area of interesting operation points.
Whereas the SOM codebook vectors are local averages of the training data, PCA represents also the first-order terms of the data. By restricting the input space of PCA to one Voronoi tesselation only, one can take advantage of the non-linear elasticity of SOM and its capability to partition the input space and building linear regression models with PCA.
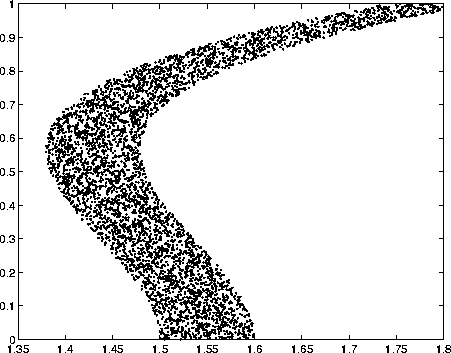
Figure 4.3: The training data used to train a SOM
In the Figure 4.3 5000 thousand artificially created codebook vectors are illustrated. These are used in training a SOM. In addition to replacing the 5000 data vectors with 10 codebook vectors that describe the original data, it partitions the input space.
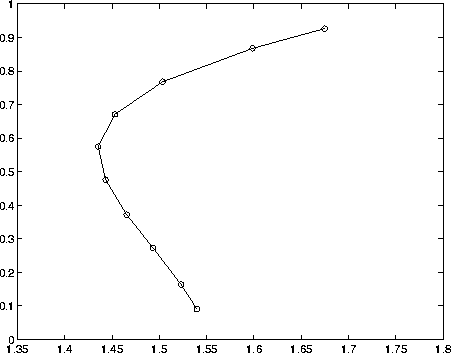
Figure 4.4: The SOM with 10 codebook vectors
The one-dimensional SOM in the Figure 4.4 quantizes the input space. Data is associated to neurons by the similarity criterion. One could build a model based on data belonging to one of the Voronoi tesselations. This kind of model would be local in nature. Neurons of the SOM are marked with small circles in the figure. The topological relationships are drawn as lines.
If the data clearly resided in a linear subspace, these local linear models could be interpreted as first derivative rules and thus be used for sensitivity analysis. Often one would like to study the behavior of a system under small changes.
The goal here is to develop methods with which one could understand the structure of the multidimensional data manifold by applying SOM to the training data and PCA to each of the Voronoi tesselations in the input space. Similar work has been reported in [5], [14], [15], [16], [17].