Principal component analysis (PCA) is a classical statistical method. This linear transform has been widely used in data analysis and compression. The following presentation is adapted from [9]. Some of the texts on the subject also include [30], [31]. Principal component analysis is based on the statistical representation of a random variable. Suppose we have a random vector population x, where
![]()
and the mean of that population is denoted by
![]()
and the covariance matrix of the same data set is
![]()
The components of ![]() , denoted by
, denoted by ![]() , represent the
covariances between the random variable components
, represent the
covariances between the random variable components ![]() and
and ![]() .
The component
.
The component ![]() is the variance of the component
is the variance of the component ![]() . The
variance of a component indicates the spread of the component values
around its mean value. If two components
. The
variance of a component indicates the spread of the component values
around its mean value. If two components ![]() and
and ![]() of the data
are uncorrelated, their covariance is zero
of the data
are uncorrelated, their covariance is zero ![]() .
The covariance matrix is, by definition, always symmetric.
.
The covariance matrix is, by definition, always symmetric.
From a sample of vectors ![]() , we can
calculate the sample mean and the sample covariance matrix as the
estimates of the mean and the covariance matrix.
, we can
calculate the sample mean and the sample covariance matrix as the
estimates of the mean and the covariance matrix.
From a symmetric matrix such as the covariance matrix, we can
calculate an orthogonal basis by finding its eigenvalues and
eigenvectors. The eigenvectors ![]() and the corresponding
eigenvalues
and the corresponding
eigenvalues ![]() are the solutions of the equation
are the solutions of the equation
![]()
For simplicity
we assume that the ![]() are distinct. These values can be
found, for example, by finding the solutions of the characteristic
equation
are distinct. These values can be
found, for example, by finding the solutions of the characteristic
equation
![]()
where the ![]() is
the identity matrix having the same order than
is
the identity matrix having the same order than ![]() and the
|.| denotes the determinant of the matrix. If the data vector has
n components, the characteristic equation becomes of order n. This
is easy to solve only if n is small. Solving eigenvalues and
corresponding eigenvectors is a non-trivial task, and many methods
exist. One way to solve the eigenvalue problem is to use a neural
solution to the problem [30]. The data is fed as the input,
and the network converges to the wanted solution.
and the
|.| denotes the determinant of the matrix. If the data vector has
n components, the characteristic equation becomes of order n. This
is easy to solve only if n is small. Solving eigenvalues and
corresponding eigenvectors is a non-trivial task, and many methods
exist. One way to solve the eigenvalue problem is to use a neural
solution to the problem [30]. The data is fed as the input,
and the network converges to the wanted solution.
By ordering the eigenvectors in the order of descending eigenvalues (largest first), one can create an ordered orthogonal basis with the first eigenvector having the direction of largest variance of the data. In this way, we can find directions in which the data set has the most significant amounts of energy.
Suppose one has a data set of which the sample mean and the covariance
matrix have been calculated. Let ![]() be a matrix consisting of
eigenvectors of the covariance matrix as the row vectors.
be a matrix consisting of
eigenvectors of the covariance matrix as the row vectors.
By transforming a data vector x, we get
![]()
which is a point in the orthogonal coordinate
system defined by the eigenvectors. Components of y can be seen
as the coordinates in the orthogonal base. We can reconstruct the
original data vector ![]() from
from ![]() by
by
![]()
using the property of an
orthogonal matrix ![]() . The
. The ![]() is the
transpose of a matrix
is the
transpose of a matrix ![]() . The original vector
. The original vector ![]() was
projected on the coordinate axes defined by the orthogonal basis. The
original vector was then reconstructed by a linear combination of the
orthogonal basis vectors.
was
projected on the coordinate axes defined by the orthogonal basis. The
original vector was then reconstructed by a linear combination of the
orthogonal basis vectors.
Instead of using all the eigenvectors of the covariance matrix, we may
represent the data in terms of only a few basis vectors of the
orthogonal basis. If we denote the matrix having the K first
eigenvectors as rows by ![]() , we can create a similar
transformation as seen above
, we can create a similar
transformation as seen above
![]()
and
![]()
This means that we project the original data vector on the coordinate axes having the dimension K and transforming the vector back by a linear combination of the basis vectors. This minimizes the mean-square error between the data and this representation with given number of eigenvectors.
If the data is concentrated in a linear subspace, this provides a way to compress data without losing much information and simplifying the representation. By picking the eigenvectors having the largest eigenvalues we lose as little information as possible in the mean-square sense. One can e.g. choose a fixed number of eigenvectors and their respective eigenvalues and get a consistent representation, or abstraction of the data. This preserves a varying amount of energy of the original data. Alternatively, we can choose approximately the same amount of energy and a varying amount of eigenvectors and their respective eigenvalues. This would in turn give approximately consistent amount of information in the expense of varying representations with regard to the dimension of the subspace.
We are here faced with contradictory goals: On one hand, we should simplify the problem by reducing the dimension of the representation. On the other hand we want to preserve as much as possible of the original information content. PCA offers a convenient way to control the trade-off between loosing information and simplifying the problem at hand.
As it will be noted later, it may be possible to create piecewise linear models by dividing the input data to smaller regions and fitting linear models locally to the data.
Now, consider a small example showing the characteristics of the eigenvectors. Some artificial data has been generated, which is illustrated in the Figure 3.1. The small dots are the points in the data set.
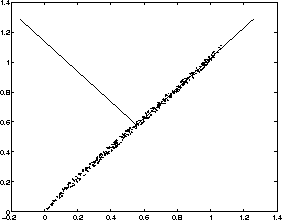
Figure 3.1: Eigenvectors of the artificially created data
Sample mean and sample covariance matrix can easily be calculated from
the data. Eigenvectors and eigenvalues can be calculated from the
covariance matrix. The directions of eigenvectors are drawn in the
Figure as lines. The first eigenvector having the largest eigenvalue
points to the direction of largest variance (right and upwards)
whereas the second eigenvector is orthogonal to the first one
(pointing to left and upwards). In this example the first eigenvalue
corresponding to the first eigenvector is ![]() while
the other eigenvalue is
while
the other eigenvalue is ![]() . By comparing the values
of eigenvalues to the total sum of eigenvalues, we can get an idea how
much of the energy is concentrated along the particular eigenvector.
In this case, the first eigenvector contains almost all the energy.
The data could be well approximated with a one-dimensional
representation.
. By comparing the values
of eigenvalues to the total sum of eigenvalues, we can get an idea how
much of the energy is concentrated along the particular eigenvector.
In this case, the first eigenvector contains almost all the energy.
The data could be well approximated with a one-dimensional
representation.
Sometimes it is desirable to investigate the behavior of the system
under small changes. Assume that this system, or phenomenon is
constrained to a n-dimensional manifold and can be approximated with
a linear manifold. Suppose one has a small change along one of the
coordinate axes in the original coordinate system. If the data from
the phenomenon is concentrated in a subspace, we can project this
small change ![]() to the approximative subspace built
with PCA by projecting
to the approximative subspace built
with PCA by projecting ![]() on all the basis vectors in
the linear subspace by
on all the basis vectors in
the linear subspace by
![]()
where the matrix ![]() has the K first eigenvectors as
rows. Subspace has then a dimension of K.
has the K first eigenvectors as
rows. Subspace has then a dimension of K. ![]() represents the change caused by the original small change. This can be
transformed back with a change of basis by taking a linear combination
of the basis vectors by
represents the change caused by the original small change. This can be
transformed back with a change of basis by taking a linear combination
of the basis vectors by
![]()
Then, we get the typical change in the real-world coordinate system
caused by a small change ![]() by assuming that the
phenomenon constrains the system to have values in the limited
subspace only.
by assuming that the
phenomenon constrains the system to have values in the limited
subspace only.