Predictable factors and state-space models

Models are tools which enable making inferences based on observations. One of their most important applications is prediction. The model can be used to infer the expected state of the world in the future or predict the expected consequences of various actions.

In unsupervised learning, the goal is to find a compact representation for the observations. The benefit is that it is often easier to find the connection between two subsets of observations using the compact representations than directly between the observations. In this case we are interested in the connection which can be made in the temporal domain.

NLFA can find compact representation for the observations. It does not take into account the temporal behaviour of the observations, but it can be expected that it is often easier to predict the future factors from the past factors than directly the future observations from the past observations. It would therefore be possible to first use NLFA to find a compact representation for observations x(t) in terms of factors s(t) and then find the mapping from the past factors s(t-1), s(t-2), $\ldots$, to the current factor s(t).

The drawback of this approach would be that in the first stage, learning does not explicitly aim at finding factors which facilitate the prediction. This can be remedied simply by combining the stages and letting the learning of factors take into account both the accuracy of description of the observations and the prediction of future factors.

  

Figure 1: The causal relations assumed by the model are depicted by solid arrows. Observations x(1), $\ldots$, x(t), $\ldots$ give information about the values of the factors. The flow of information to the factor s(t) is represented by dashed arrows. Bayes' rule is used for reversing the arrows.

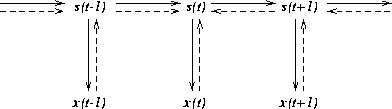The model defined by (1) and (2) does exactly this. Learning of factors s(t) takes into account three sources of information: 1) the factors should be able to represent the observations x(t), 2) the factors should be able to predict the factors s(t+1) at the next time step and 3) the factors should be well predicted by the factors s(t-1)at the previous time step. This is depicted in figure 1.

As (2) shows, the model assumes that the factors s(t) can be predicted from the immediately preceding factors s(t-1) without knowing the factors in the more distant past. This does not restrict the class of dynamical processes which can be modelled because any model with long range dependencies can be converted into an equivalent model with only one step dependencies but larger number of factors. This means that the factors store all the information needed for predicting the dynamic behaviour of the process and therefore the factors can be interpreted as the state of the dynamical system.

  

Figure 2: (a) The factor s(t) depends on the three previous values s(t-3), s(t-2) and s(t-1). (b) This dynamics can be transformed into an equivalent state representation where s₁(t) corresponds to s(t) while s₂(t) and s₃(t) store the values s(t-1) and s(t-2), respectively.

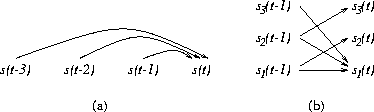Figure 2 gives an example about how a model with three step delays can be transformed into an equivalent state representation with only one step delays but more factors. In this case the two extra factors s₂(t) and s₃(t) store the values s(t-1) and s(t-2), but they could, for instance, store the first and second time derivatives of s(t) as well. The benefit of using the state representation is that the model can learn the structure of the memory.