

Next: Discussion
Up: Results
Previous: Finding the underlying process
An obvious way to assess the quality of the learned model is to see on
how long term the predictions given by the model are accurate. It
should be noted that since the Lorenz process is chaotic, it is
numerically impossible to predict it exactly in the distant future.
The best that can be hoped for is to capture the overall aspects of
the long-term behaviour. Figure 6 confirms that this
is accomplished by the NDFA algorithm.
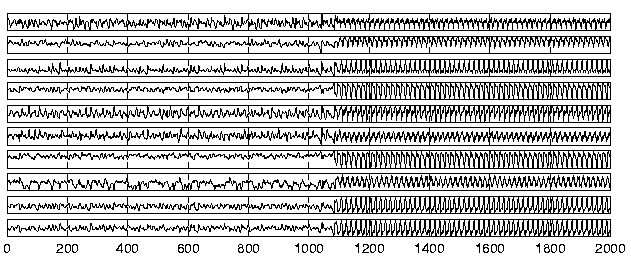
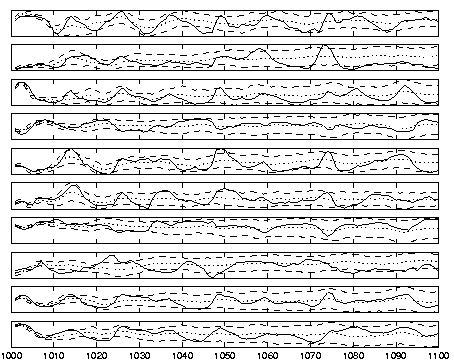
Figure 7:
The ten plots show the original observations
x(t)
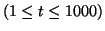 and the result of prediction made by a
nonlinear auto-regressive model
and the result of prediction made by a
nonlinear auto-regressive model
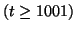 .
The noise
process was omitted like in the results shown in figures
5 and 6.
.
The noise
process was omitted like in the results shown in figures
5 and 6.
 |
For comparison, the prediction of the future observations was tested
with a nonlinear auto-regressive (NAR) model
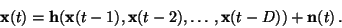 |
(19) |
Several strategies were tested and the best performance was given by
an MLP network with 20 inputs and one hidden layer of 30 neurons. The
inputs to the MLP network were the principal components extracted from
the sequence of ten past observations, that is, D was ten.
Figure 7 shows the performance of this NAR model. It
is evident that the prediction of new observations is a challenging
problem. Principal component analysis used in the model can extract
features which are useful in predicting the future observations but
clearly the features are not good enough for modelling the long-term
behaviour of the observations.
Figure 8:
The average cumulative squared prediction error is computed for
the predictions made using the NDFA algorithm after 7500 (dotted
with triangles), 30,000 (dash-dotted), 150,000 (dashed) and and
600,000 iterations (solid) as well as by a nonlinear
auto-regressive model (solid with dots). The predictions are
based on 100 Monte-Carlo simulations of the estimated dynamics.
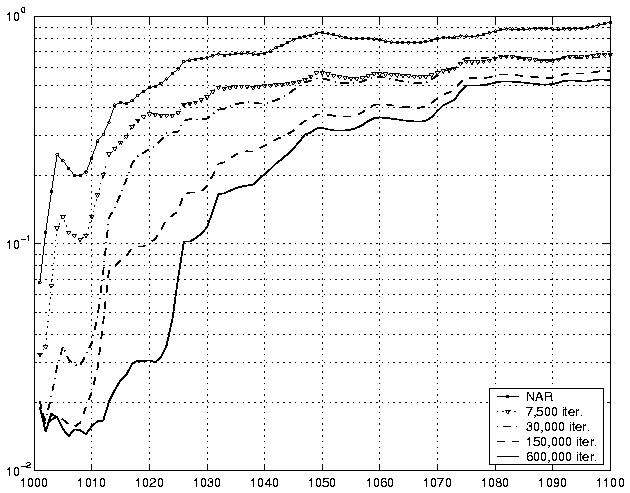
Taking into consideration the observation noise whose variance is
0.01, the prediction obtained by the NDFA algorithm in the end of
learning is excellent up to t = 1010 and fairly good up to t =
1022. The NAR model is quite inaccurate already after
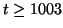 .
.
 |
Both the NAR model and the model used in NDFA algorithm contain noise
process which can be taken into account in the prediction by
Monte-Carlo simulation. Figure 8 shows the results
obtained by 100 runs of Monte-Carlo simulation. The average predicted
observations are compared to the actual continuation of the process.
The figure shows the average cumulative squared prediction error.
Since the variance of the noise on the observations is 0.01, the
results can be considered perfect if the average squared prediction
error is 0.01. The signal variance is 1, which gives the practical
upper bound of the prediction accuracy. The figure confirms that the
NDFA algorithm has been able to model the dynamics of the process as
the short-term average prediction error is close to the noise
variance. Even the long-term prediction falls below the signal
variance which indicates that at least some part of the process can be
predicted in the more distant future. The steady progress made during
learning is also evident.
Figure 9:
The factors
s(t) have been predicted by Monte-Carlo
simulations. The mean 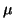 (dashed) and range
(dashed) and range
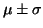 (solid) obtained from the simulation runs are shown.
(solid) obtained from the simulation runs are shown.
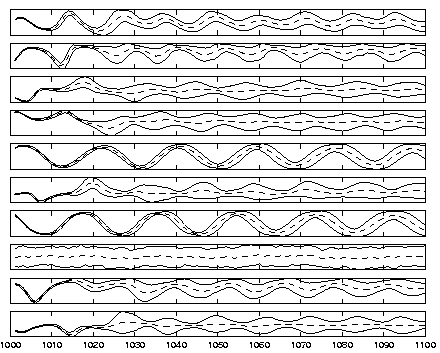 |
Figure 10:
The factors in figure 9 are mapped on the original
state space. The mean (dotted) and range (dashed) together with
the true continuation (solid) are shown. Due to the chaotic
nature of the Lorenz system, the state cannot be predicted for
distant future. Notice, however, how the model has been able to
predict the timing of the oscillations for the first and fourth
states although the sign is uncertain.
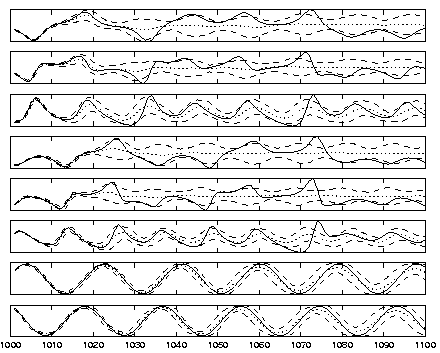 |
Figure 11:
The factors in figure 9 are projected onto the
observations by the estimated mapping
f. The mean
(dotted) and range (dashed) together with the true continuation
(solid) are shown.
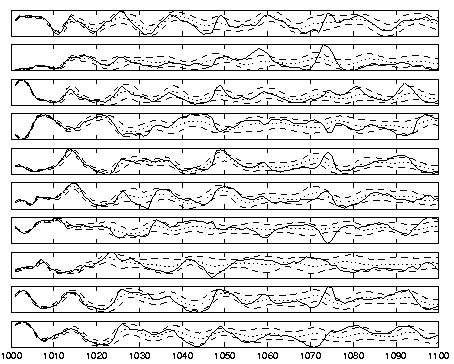 |
Figure 12:
Monte-Carlo simulations with the NAR model have been used for
predicting the observations. The mean (dotted) and range (dashed)
together with the true continuation (solid) are shown.
 |
Figures 9-12 show the results of the
Monte-Carlo simulations for individual time series. Each plot shows
the averages 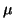 and the range
and the range
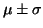 as obtained from the
simulations. Here
as obtained from the
simulations. Here 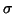 stands for the standard deviation. Figure
9 depicts the predicted continuation of the factors
s(t). In figure 10, these are mapped to the
original state space while figures 11 and
12 show the predicted observations obtained by the
NDFA algorithm and NAR model, respectively, together with the true
continuation.
stands for the standard deviation. Figure
9 depicts the predicted continuation of the factors
s(t). In figure 10, these are mapped to the
original state space while figures 11 and
12 show the predicted observations obtained by the
NDFA algorithm and NAR model, respectively, together with the true
continuation.


Next: Discussion
Up: Results
Previous: Finding the underlying process
Harri Valpola
2000-10-17







![]() and the range
and the range
![]() as obtained from the
simulations. Here
as obtained from the
simulations. Here ![]() stands for the standard deviation. Figure
9 depicts the predicted continuation of the factors
s(t). In figure 10, these are mapped to the
original state space while figures 11 and
12 show the predicted observations obtained by the
NDFA algorithm and NAR model, respectively, together with the true
continuation.
stands for the standard deviation. Figure
9 depicts the predicted continuation of the factors
s(t). In figure 10, these are mapped to the
original state space while figures 11 and
12 show the predicted observations obtained by the
NDFA algorithm and NAR model, respectively, together with the true
continuation.