


Next: Bayes' rule
Up: BAYESIAN PROBABILITY THEORY
Previous: Propositions
Bayesian probability theory can be conveniently summarised in the
following elementary rules:
- Sum rule:
-
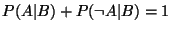
- Product rule:
-
P(AB | C) = P(A | C) P(B | AC)
Here P(A | B) denotes the probability of A on the condition that
B is true. These rules correspond to the negation and conjunction
operations of Boolean algebra. The disjunction does not need a
separate rule because it can be derived from negation and conjunction:
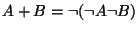 . In fact, only one operation would
suffice since other operations can be derived from either NAND or NOR
operation alone. The NAND operation, for instance, yields the
following rule, starting from which every other rule of Bayesian
probability theory can be derived:
. In fact, only one operation would
suffice since other operations can be derived from either NAND or NOR
operation alone. The NAND operation, for instance, yields the
following rule, starting from which every other rule of Bayesian
probability theory can be derived:
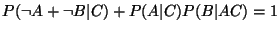 .
.
These rules fix the scale on which the degrees of belief are measured.
Cox showed that under very general requirements of consistency and
compatibility with common sense, the rules of calculus with beliefs
have to be homomorphic with the sum and product rule [19]. This
means that one can measure the degrees of beliefs on any scale, but it
is possible to transform the degrees of beliefs on the canonical scale
of probabilities such that the rules for negation and conjunction take
the form of the sum and product rule.



Next: Bayes' rule
Up: BAYESIAN PROBABILITY THEORY
Previous: Propositions
Harri Valpola
2000-10-31