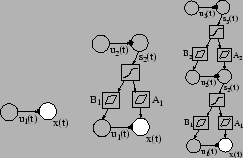Hierarchical Nonlinear Variance Model

Figure 4 shows the structure for the hierarchical nonlinear variance (HNV) model. It utilises variance neurons and nonlinearities in building a hierarchical model for both the means and variances. Without the variance neurons the model would correspond to a multi-layer perceptron with latent variables at hidden neurons. Note that computation nodes as hidden neurons would result in multiple paths from upper layer latent variables to the observations. This type of structure was used in [5] and it has a quadratic as opposed to linear computational complexity.

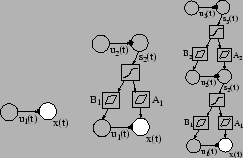Figure: HNV model can be built up in stages. Left: A variance neuron is attached to each Gaussian observation node. The nodes represent vectors. Middle: A layer of sources with variance neurons attached to them is added. The nodes next to the weight matrices $\mathbf{A}_{1}$ and $\mathbf{B}_{1}$ represent affine transformations including a bias term. Right: Another layer is added. The size of the layers may vary. More layers can be added in the same manner.