Results

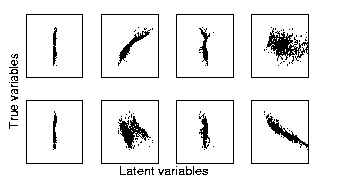
Several different structures were tested for the network and the best one was chosen according to the probability mass it occupied in the posterior pdf of all models. The most probable model had four latent variables and ten hidden units. Despite the difficulty of the problem, the network was able to discover the underlying causes of the observations. Out of the four latent variables, two corresponded to the original inputs that had generated the data while the other two had much smaller variances and were used by the network to represent the slight discrepancies between the original and the estimated nonlinear generative models. Notice that the two models used different nonlinearities and therefore can never be exactly the same.

Figure 1 shows the scatter plots of the four estimated latent variables (x-axes) versus the two original inputs (y-axes). The first original input (upper row) correlated with the second latent variable while the second original input correlated with the fourth latent variable. The figure shows that the first and third latent variables had much smaller variance than the two others.

For comparison, four independent components extracted by linear ICA ¹ are shown in similar scatter plots in figure 2. As the data is severely nonlinear, linear ICA performs very poorly. None of the retrieved sources correspond to the original inputs and all four sources are used for representing the data. These results show that the nonlinearity was quite strong and, consequently, the problem of finding the underlying latent variables very difficult.

  

Figure 1: Scatter plots of the two original inputs and the posterior means of the four estimated latent variables.

  

Figure 2: Scatter plots of the original inputs and the four sources estimated by linear ICA.