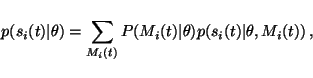 |
(33) |
The nonlinear factor analysis model introduced in the previous section has Gaussian distributions for the sources. In this section we are going to show how that model can easily be extended to have mixture-of-Gaussians models for sources. In doing so we are largely following the method introduced in [1] for Bayesian linear independent factor analysis. The resulting model is a nonlinear counterpart of ICA or, more accurately, a nonlinear counterpart of independent factor analysis because the model includes finite noise. The difference between the models is similar to that between linear PCA and ICA because the first layer weight matrix A in the network has the same indeterminacies in nonlinear PCA as in linear PCA. The indeterminacy is discussed in the introductory chapter.
According to the model for the distribution of the sources, there are
several Gaussian distributions and at each time instant, the source
originates from one of them. Let us denote the index of the Gaussian
from which the source si(t) originates by Mi(t).
The model for the distribution for the ith source at time t is
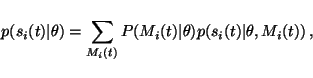 |
(33) |
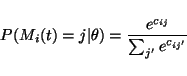 |
(34) |
Each combination of different Gaussians producing the sources can be
considered a different model. The number of these models is enormous,
of course, but their posterior distribution can still be approximated
by a similar factorial approximation which is used for other
variables.
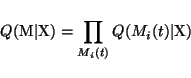 |
(35) |
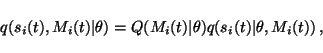 |
(36) |
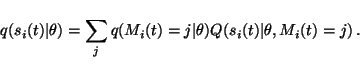 |
(37) |
Due to the assumption of factorial posterior distribution of the
models, the cost function can be computed as easily as before. Let us
denote
![]() and the posterior
mean and variance of
and the posterior
mean and variance of
![]() by
by
![]() and
and
![]() .
It easy to see that the
posterior mean and variance of si(t) are
.
It easy to see that the
posterior mean and variance of si(t) are
![\begin{multline}q(s_i(t) \vert \mathrm{X}) \ln q(s_i(t) \vert \mathrm{X}) = \\ \...
...(t) = j, \mathrm{X}) \ln q(s_i(t) \vert
M_i(t) = j, \mathrm{X})]
\end{multline}](img105.gif)
Most update rules are the same as for nonlinear factor analysis.
Equations (39) and (40) bring the terms
![]() for updating the means mij and log-std
parameters vij of the sources. It turns out that they both will
be weighted with
for updating the means mij and log-std
parameters vij of the sources. It turns out that they both will
be weighted with
![]() ,
i.e., the observation is used for
adapting the parameters in proportion to the posterior probability of
that observation originating from that particular Gaussian
distribution.
,
i.e., the observation is used for
adapting the parameters in proportion to the posterior probability of
that observation originating from that particular Gaussian
distribution.