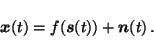 |
(1) |
The linear principal and independent component analysis (PCA and ICA) model the data as having been generated by independent sources through a linear mapping. The difference between the two is that PCA restricts the distribution of the sources to be Gaussian, whereas ICA does not, in general, restrict the distribution of the sources.
In this chapter we introduce nonlinear counterparts of PCA and ICA
where the generative mapping form sources to data is not restricted to
be linear. The general form of the models discussed here is
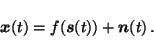 |
(1) |
Just as their linear counterparts, the nonlinear versions of PCA and ICA can be used for instance in dimension reduction and feature extraction. The difference between linear and nonlinear PCA is depicted in Fig. 1. In the linear PCA the data is described with a linear coordinate system whereas in the nonlinear PCA the coordinate system is nonlinear. The nonlinear PCA and ICA can be used for similar tasks as their linear counterparts, but they can be expected to capture the structure of the data better if the data points lie in a nonlinear manifold instead of a linear subspace.
![\includegraphics[width=11.7cm]{nonlin.eps}](img6.gif) |
Usually the linear PCA and ICA models do not have an explicit noise
term
![]() and the model is thus simply
and the model is thus simply
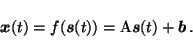 |
(2) |
In this chapter, the distribution of sources is modelled with Gaussian density in PCA and mixture-of-Gaussians density in ICA. Given enough Gaussians in the mixture, any density can be modelled with arbitrary accuracy using the mixture-of-Gaussians density, which means that the source density model is universal. Likewise, the nonlinear mapping f() is modelled by a multi-layer perceptron (MLP) network which can approximate any nonlinear mapping with arbitrary accuracy given enough hidden neurons.
The noise on each observation channel (component of data vectors) is assumed to be independent and Gaussian, but the variance of the noise on different channels is not assumed to be equal. The noise could be modelled with a more general distribution, but we shall restrict the discussion to the simple Gaussian case. After all, noise is supposed to be something uninteresting and unstructured. If the noise is not Gaussian or independent, it is a sign of interesting structure which should be modelled by the generative mapping from the sources.