In order to apply the Bayesian approach for modelling, the model needs to be given in probabilistic terms, which means stating the joint distribution of all the variables in the model. In principle, any joint distribution can be regarded as a model, but in practice, the joint distribution will have a simple form.
As an example, we shall see how a generative model turns into a
probabilistic model. Suppose we have a model which tells how a
sequence
![]() transforms into sequence
transforms into sequence
![]() .
.
If y(t) and ![]() are given, then x(t) has the same
distribution as n(t) except that it is offset by
are given, then x(t) has the same
distribution as n(t) except that it is offset by
![]() .
This means that if n(t) is Gaussian noise with variance
.
This means that if n(t) is Gaussian noise with variance ![]() ,
equation 14 translates into
,
equation 14 translates into
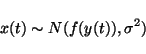 |
(15) |
![\begin{displaymath}p(x(t) \vert y(t), \theta, \sigma) = \frac{1}{\sqrt{2\pi\sigma^2}}
e^{-\frac{[x(t) - f(y(t), \theta)]^2}{2\sigma^2}} \, .
\end{displaymath}](img58.gif) |
(16) |
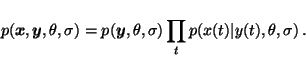 |
(17) |
In supervised learning, the sequence ![]() is assumed to be fully
known, also for any future data, which means that the full joint
probability
is assumed to be fully
known, also for any future data, which means that the full joint
probability
![]() is not needed, only
is not needed, only
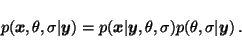 |
(18) |
If the probability
![]() is not modelled in supervised
learning, it is impossible to treat missing elements of the sequence
is not modelled in supervised
learning, it is impossible to treat missing elements of the sequence
![]() .
If the probability
.
If the probability
![]() is modelled, however,
there are no problems. The posterior density is computed for all
unknown variables, including the missing elements of
is modelled, however,
there are no problems. The posterior density is computed for all
unknown variables, including the missing elements of ![]() .
In
fact, unsupervised learning can be seen as a special case where the
whole sequence
.
In
fact, unsupervised learning can be seen as a special case where the
whole sequence ![]() is unknown. In probabilistic framework, the
treatment of any missing values is possible as long as the model
defines the joint density of all the variables in the model. It is,
for instance, easy to treat missing elements of sequence
is unknown. In probabilistic framework, the
treatment of any missing values is possible as long as the model
defines the joint density of all the variables in the model. It is,
for instance, easy to treat missing elements of sequence ![]() or
mix freely between supervised and unsupervised learning depending on
how large part of the sequence
or
mix freely between supervised and unsupervised learning depending on
how large part of the sequence ![]() is known.
is known.