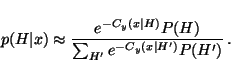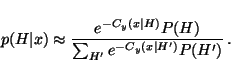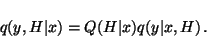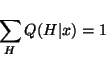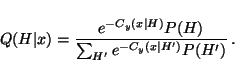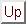

Next: Connection to coding
Up: Ensemble learning
Previous: Ensemble learning
Recall that the cost function
Cy(x | H) can be translated into
lower bound for p(x | H). Since
p(H | x) = p(x | H) p(H) / p(x),
it is natural that
Cy(x | H) can be used for model selection also
by equating
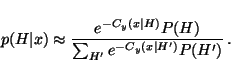 |
(7) |
In fact, we can show that the above equation gives the best
approximation for p(H | x) in terms of
Cy, H(x), the
Kullback-Leibler divergence between
q(y, H | x) and
p(y, H | x),
which means that the model selection can be done using the same
principle of approximating the posterior distribution as learning
parameters.
Without losing any generality from
q(y, H | x), we can write
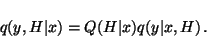 |
(8) |
Now the cost function can be written as
Minimising
Cy, H(x) with respect to Q(H | x) under the constraint
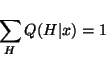 |
(10) |
yields
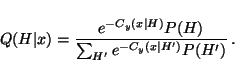 |
(11) |
Substituting this into equation 9 yields the minimum
value for
Cy, H(x) which is
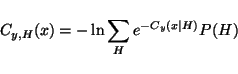 |
(12) |
If we wish to use only a part of different model structures H, we
can try to find those H which would minimise
Cy, H(x). It is
easy to see that this is accomplished by choosing the models
corresponding to
Cy(x | H). A special case is to use only one Hcorresponding to the smallest
Cy(x | H).


Next: Connection to coding
Up: Ensemble learning
Previous: Ensemble learning
Harri Lappalainen
2000-03-03