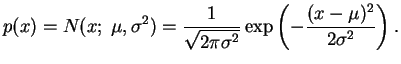 |
(A.1) |
The normal distribution, which is also known as the Gaussian distribution, is ubiquitous in statistics. The averages of identically distributed random variables are approximately normally distributed by the central limit theorem, regardless of their original distribution[16]. This section concentrates on the univariate normal distribution, as the general multivariate distribution is not needed in this thesis.
The probability density of the normal distribution is given by
The multivariate case is very similar:
By the definition of the variance
The negative differential entropy of the normal distribution can be evaluated simply as
Another important expectation for our purposes is [35]
A plot of the probability density function of the normal distribution is shown in Figure A.1.
![\includegraphics[width=.5\textwidth]{pics/gauss}](img498.gif)
|