NATURAL GRADIENT ASCENT

The natural gradient learning algorithm is analogous to conventional gradient ascent algorithm and is given by the iteration

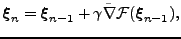$$\boldsymbol{\xi}_n = \boldsymbol{\xi}_{n-1} + \gamma \tilde{\nabla} \mathcal{F}(\boldsymbol{\xi}_{n-1}),$$ (17)

where the step size 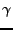$\gamma$ can either be adjusted adaptively during learning or computed for each iteration using e.g. line search (Amari, 1998). This line search should be performed or any longer step taken along a suitable geodesic, which is a length minimizing curve and therefore the Riemannian counterpart of a straight line. In practice, geodesics are often approximated with straight lines (Amari, 1998), as natural gradient ascent is typically applied to problems with complex geometries, and the geodesics on such manifolds can be hard to derive and compute.

In general, the performance of natural gradient learning is superior to conventional gradient learning when the problem space is Riemannian. For instance, natural gradient learning can often avoid the plateaus present in conventional gradient learning (Amari, 1998).