


Next: About this document
Up: No Title
Previous: No Title
-
Determine whether the following propositional formulas are satisfiable:
-
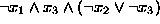 ;
; -
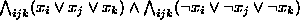 .
.
In formula (b), the indexing is over all triples (i, j, k) such
that 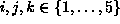 and
and 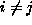 ,
, 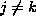 ,
, 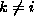 .
. -
Suppose that SAT
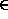 P. Show that there then exists a polynomial
time algorithm that for each formula
P. Show that there then exists a polynomial
time algorithm that for each formula 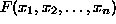 either
states that the formula is not satisfiable, or actually finds a
satisfying truth assignment to the variables
either
states that the formula is not satisfiable, or actually finds a
satisfying truth assignment to the variables 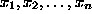 .
(Hint: It is easy to see that
formula
.
(Hint: It is easy to see that
formula 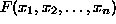 is satisfiable, if and only if
either formula
is satisfiable, if and only if
either formula 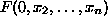 or formula
or formula 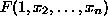 is satisfiable.)
is satisfiable.) -
Prove the following Lemmas (p. 115 of the lecture notes):
- If L is an NP-complete set and
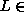 P, then P = NP.
P, then P = NP. - If L is an NP-complete set,
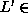 NP and
NP and
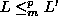 , then also L' is NP-complete.
, then also L' is NP-complete.
-
Construct a polynomial time reduction from the Clique problem
to the Vertex Cover (VC) problem. (Hint: Look at the
reductions presented on pp. 111-112 of the lecture notes.)
-
Prove that the following Set Packing problem is NP-complete:
Given a collection of subsets 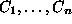 of a finite set U,
and a natural number k, is it possible to choose a subcollection
of at least k disjoint
of a finite set U,
and a natural number k, is it possible to choose a subcollection
of at least k disjoint 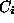 's (i.e.
's (i.e. 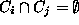 for
for 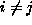 )?
)?
(Hint: Reduction from the Independent Set (IS) problem.)
Reminder: This is the last problem set. The last lecture of the
course is on Monday, 7 Dec, and the course exam takes place on Tuesday,
15 Dec (8-12).
Pekka Orponen
Thu Dec 3 15:17:23 EET 1998
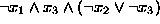 ;
;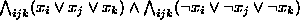 .
.
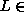 P, then P = NP.
P, then P = NP.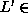 NP and
NP and
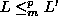 , then also L' is NP-complete.
, then also L' is NP-complete.
of a finite set U, and a natural number k, is it possible to choose a subcollection of at least k disjoint
's (i.e.
for
)?