


Next: About this document
Up: No Title
Previous: No Title
-
-
Modify Floyd's algorithm (p. 67 of the lecture notes) so that
in addition to computing the shortest distances between nodes
the algorithm also makes it possible to actually trace the
optimal paths.
(Hint: Augment the distance matrix D by another
matrix N that keeps track, for each pair of nodes (i,j),
which is the node following the start node i on the shortest
route leading to j.)
-
Simulate the behaviour of your algorithm using as input
the graph below:
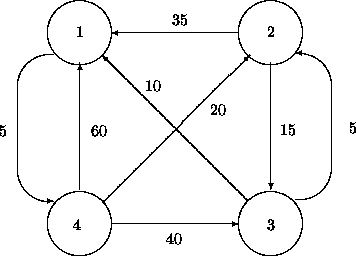
-
-
Give a recurrence equation that describes the number C(n) of binary
trees with n nodes, and based on this, a reasonably efficient
algorithm for computing values of C(n).
(Hint: A binary tree consists of a root and a left and
a right subtree.)
-
Using the method of ``generating functions''
(e.g. Cormen/Leiserson/Rivest, p. 262)
one can actually solve the above recurrence in closed form
and obtain the explicit formula
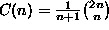 .
(The numbers C(n) are for historical reasons known
as ``Catalan numbers''.)
Estimate the order of growth of the function C(n) using
Stirling's formula
.
(The numbers C(n) are for historical reasons known
as ``Catalan numbers''.)
Estimate the order of growth of the function C(n) using
Stirling's formula
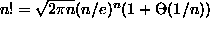 .
.
-
Try to modify Dijkstra's algorithm (p. 70 of the lecture notes)
to find the longest (noncyclic) path connecting two nodes
in a graph. Which difficulty do you meet in the algorithm?
(Additional information:
The longest path problem is NP-complete, and thus probably not
solvable by any polynomial-time algorithm.)
-
-
Simulate Kruskal's algorithm (p. 73 of the lecture notes)
for finding a minimal spanning tree of the graph below.
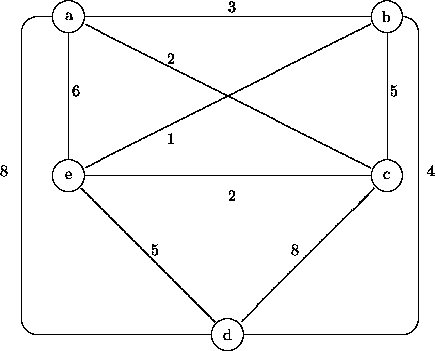
-
Simulate the behaviour of the greedy TSP heuristic (p. 75 of the notes)
on the same input graph.
Pekka Orponen
Wed Nov 18 02:25:03 EET 1998

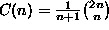 .
(The numbers C(n) are for historical reasons known
as ``Catalan numbers''.)
Estimate the order of growth of the function C(n) using
Stirling's formula
.
(The numbers C(n) are for historical reasons known
as ``Catalan numbers''.)
Estimate the order of growth of the function C(n) using
Stirling's formula
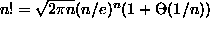 .
.
