![]()
satisfies the condition ![]() for all
for all ![]() .
.
Hint for case (a): one ``standard'' method for long-integer multiplication is the following algorithm:
multiply(x,y);{
;
y > 0
{
;
;
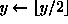
};
(z)
}
![]()
satisfies the condition ![]() for all
for all ![]() .
.
Hint for case (a): one ``standard'' method for long-integer multiplication is the following algorithm:
multiply(x,y);{
;
y > 0
{
;
;
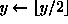
};
(z)
}