Data Structures and Algorithms 2, Fall 1998
Problem Set 1 (9-11 Nov.)

1. Arrange the following functions in an increasing sequence according to their order of growth (big-O) classes:

   

   (The notation `` '' denotes here and in the problems below base-2 logarithms.)

2. Show that

   

   (Hint: Construct an upper bound for the value of the sum using the term, and a lower bound using the term .)

3. Analyze the worst-case complexity of the following ``selection sort'' algorithm:

    
              		 selectsort(  ):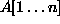
   
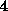         (  )		 		 for 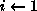   to n-1 do
   
         (  ) 		 		 {   ;   ;
   
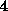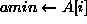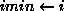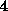         (  ) 		 		 		    for 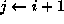   to n do
   
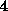         (  ) 		 		 		    		 if A[j] <  amin then
   
         (  ) 		 		 		 		 		 {  ;   }
   
         (  ) 		 		 		   ;    }
   
              		 		 }
   
   

4. Solve, by unwinding, the following recurrence equation:

   

5. Determine the order of growth (big-O) classes for the following recurrence equations. In each case the boundary condition is T(1) = 1, and the functions need to be considered only for values of n that are powers of 2. (Note: Item (d) is slightly more difficult than the others.)

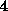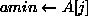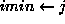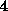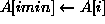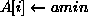   (a)

   T(n) = T(n/2) + 1,

   (b)

   T(n) = 2T(n/2) + n,

   (c)

   .

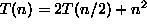   (d)

   ,

6. Analyze the worst-case complexity of the following recursive algorithm for determining the maximum and minimum elements of an array , in the case when n is a power of 2.

    
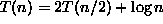             		 function   ;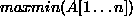
   
             		 begin
   
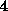        (  )		 		 if n=1 then return (A[1],A[1])
   
             		 		 else begin
   
        (  ) 		 		 		   ;
   
        (  ) 		 		 		   
   
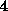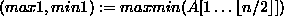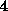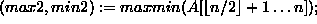
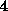        (  ) 		 		 		 return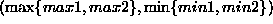   
   
             		 		 end
   
        		end   .