TIE211 Tietorakenteet ja algoritmit 2
Loppukoe ke 18.8.1999 klo 8-12

1. Oletetaan, että tunnet vaativuudeltaan kertaluokkaa 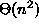olevan yksinkertaisen algoritmin jonkin ongelman ratkaisuun. Oletetaan edelleen, että tiedät miten ongelman kokoa n oleva tapaus voitaisiin palauttaa kolmeen kokoa n/2 olevaan tapaukseen, joista yhdistämällä alkuperäisen tapauksen vastaus voitaisiin muodostaa lineaarisessa ajassa. Osatapaukset voidaan muodostaa ajassa 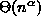. Miten pieni täytyy vakion olla, jotta osittamiseen perustuva ratkaisualgoritmi olisi tehokkaampi kuin alussa mainittu yksinkertainen algoritmi?
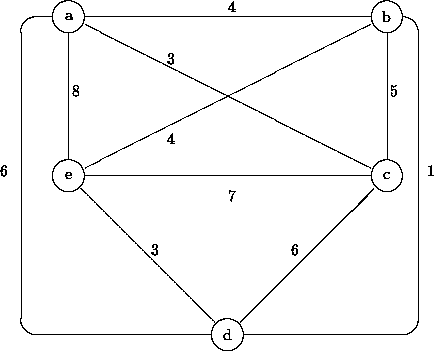
2. Simuloi kauppamatkustajan ongelman (a) ahneen ratkaisuheuristiikan, (b) Lin-Kernighan 2-vaihtoheuristiikan toimintaa oheisessa verkossa. Valitse LK-heuristiikan alkuratkaisuksi reitti abcde.

   

3. Tarkastellaan seuraavaa NP-täydellistä repunpakkausongelmaa. On annettu joukko ``tavaroita'' 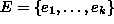ja niiden ``koot'' 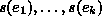ja ``arvot'' 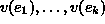sekä luonnollinen luku S (``repun tilavuus''). Tehtävänä on valita tavaroiden joukosta sellainen osakokoelm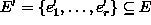a , että 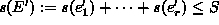(``tavarat mahtuvat reppuun'') ja ``repun arvo'' 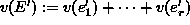on mahdollisimman suuri. Suunnittele ongelmalle (a) ahne ja (b) paikalliseen etsintään perustuva ratkaisuheuristiikka.
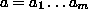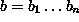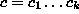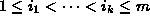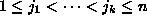4. Pisimmän yhteisen alijonon määritystehtävässä syötteenä annetaan merkkijonot ja , ja tehtävänä on määrittää suurin sellainen luku k, että jokin jono esiintyy sekä jonon a että jonon b alijonona (so. joillakin indekseillä ja on 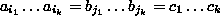). Esimerkiksi merkkijonoilla VIISAS ja SIKA on kaksikin kahden merkin mittaista yhteistä alijonoa (IA ja SA), mutta ei yhtään kolmen merkin mittaista yhteistä alijonoa; tässä tapauksessa on siis k=2. Huomaa, ettei alijonon c merkkien tarvitse esiintyä jonoissa a ja b yhtenäisesti peräkkäin. -- Laadi algoritmi, joka määrittää annettujen syötejonojen 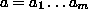ja 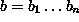pisimmän yhteisen alijonon pituuden k ajassa O(mn). (Vihje: Muodosta taulukko 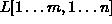, missä L[i,j] = jokin sopivasti valittu jonoihin 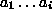ja 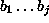liittyvä suure.)

Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.