


Next: About this document
Up: No Title
Previous: No Title
-
Järjestä seuraavat funktiot kertaluokkiensa mukaiseen kasvavaan
järjestykseen:
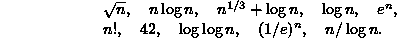
(Merkintä 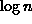 tarkoittaa tässä kaksikantaista logaritmia.)
tarkoittaa tässä kaksikantaista logaritmia.)
-
Simuloi kauppamatkustajan ongelman (a) ahneen ratkaisuheuristiikan,
(b) Lin-Kernighan 2-vaihtoheuristiikan toimintaa oheisessa verkossa.
Valitse LK-heuristiikan alkuratkaisuksi reitti abcde.
-
NP-täydellisessä riippumaton joukko -ongelmassa (engl.\
Independent Set) on tehtävänä löytää annetusta
suuntaamattomasta verkosta mahdollisimman suuri solmujoukko, jossa
minkään solmuparin välillä ei ole kaarta. Suunnittele ongelmalle (a) ahne,
(b) paikalliseen etsintään perustuva ratkaisuheuristiikka ja anna esimerkit
niiden toiminnasta. Miten soveltaisit ns. simuloitua jäähdytystä
tämän ongelman tapauksessa?
-
Ns. Hanoin tornit -ongelmassa tehtävänä on siirtää
n halkaisijaltaan erikokoisen puukiekon pino yksi kerrallaan
kolmen aluslautaan kiinnitetyn puikon kesken siten, että kiekot
siirtojonon alussa ovat järjestyksessä vasemmanpuoleisessa
puikossa, siirtojonon lopussa samoin järjestyksessä oikeanpuoleisessa
puikossa, ja missään siirtovaiheessa ei isompaa kiekkoa sijoiteta pienemmän
päälle. (Ks. kuva.)
-
Olkoon annettuna alkeissiirto-operaatio s(i,j), joka siirtää yhden
kiekon puikon i päältä puikon j päälle.
Suunnittele tähän operaatioon perustuen osittava algoritmi
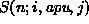 , joka siirtää (laillisesti!) n kiekon pinon
puikosta i puikkoon j käyttäen ``välilaskupaikkana'' puikkoa
, joka siirtää (laillisesti!) n kiekon pinon
puikosta i puikkoon j käyttäen ``välilaskupaikkana'' puikkoa 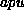 .
(Vihje: Aloita siirtämällä n-1 päällimmäistä kiekkoa puikosta
i puikkoon
.
(Vihje: Aloita siirtämällä n-1 päällimmäistä kiekkoa puikosta
i puikkoon 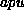 .)
Erityisesti siis algoritmin kutsu S(n;1,2,3) ratkaisee alkuperäisen
n kiekon torniongelman. Esimerkiksi kahden kiekon tapauksessa kutsun
S(2;1,2,3) tulisi tuottaa alkeissiirtojono ``s(1,2); s(1,3); s(2,3)''.
.)
Erityisesti siis algoritmin kutsu S(n;1,2,3) ratkaisee alkuperäisen
n kiekon torniongelman. Esimerkiksi kahden kiekon tapauksessa kutsun
S(2;1,2,3) tulisi tuottaa alkeissiirtojono ``s(1,2); s(1,3); s(2,3)''. -
Muodosta rekursioyhtälö, joka kuvaa algoritmin kutsun
S(n;1,2,3) tuottamien yhden kiekon alkeissiirtojen määrää
n:n funktiona. Ratkaise yhtälö.
Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.
Pekka Orponen
Wed Mar 24 10:55:59 EET 1999
![]()
![]() tarkoittaa tässä kaksikantaista logaritmia.)
tarkoittaa tässä kaksikantaista logaritmia.)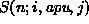 , joka siirtää (laillisesti!) n kiekon pinon
puikosta i puikkoon j käyttäen ``välilaskupaikkana'' puikkoa
, joka siirtää (laillisesti!) n kiekon pinon
puikosta i puikkoon j käyttäen ``välilaskupaikkana'' puikkoa 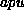 .
(Vihje: Aloita siirtämällä n-1 päällimmäistä kiekkoa puikosta
i puikkoon
.
(Vihje: Aloita siirtämällä n-1 päällimmäistä kiekkoa puikosta
i puikkoon 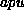 .)
Erityisesti siis algoritmin kutsu S(n;1,2,3) ratkaisee alkuperäisen
n kiekon torniongelman. Esimerkiksi kahden kiekon tapauksessa kutsun
S(2;1,2,3) tulisi tuottaa alkeissiirtojono ``s(1,2); s(1,3); s(2,3)''.
.)
Erityisesti siis algoritmin kutsu S(n;1,2,3) ratkaisee alkuperäisen
n kiekon torniongelman. Esimerkiksi kahden kiekon tapauksessa kutsun
S(2;1,2,3) tulisi tuottaa alkeissiirtojono ``s(1,2); s(1,3); s(2,3)''.