TIE211 Tietorakenteet ja algoritmit 2
Loppukoe ke 20.1.1999 klo 8-12

1. Laadi algoritmi, jonka suoritusaikaa vakiotekijöitä lukuunottamatta kuvaa rekursioyhtälö

   

   Algoritmi saa syötteenään n-alkioisen taulukon A[1..n], mutta sillä, mitä algoritmi varsinaisesti tekee, ei ole merkitystä. Määritä em. rekursioyhtälön ratkaisun kertaluokka, kun n on kahden potenssi.

2. Ns. Eulerin luku ilmaisee, monessako joukon permutaatiossa on tasan k nousua, so. positiota i joissa . Luvut voidaan laskea rekursioyhtälöstä:

   

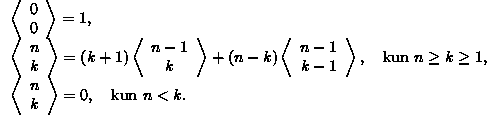
   Laadi em. kaavoihin perustuva kohtuullisen tehokas algoritmi luvun määrittämiseksi. Mikä on algoritmisi aika- ja tilavaativuus?

3. Suunnittele peruuttava algoritmi ns. n kuningattaren ongelman ratkaisemiseen: -shakkilaudalle on sijoitettava (mikäli mahdollista) n kuningatarta niin, että ne eivät uhkaa toisiaan, so. niin että mitkään kaksi nappulaa eivät ole keskenään samalla laudan rivillä, sarakkeella eivätkä diagonaalilla. Mikä on algoritmisi aikavaativuus?
4. Määrittele seuraavat käsitteet: ongelmaluokka NP, polynominen palautus, NP-täydellinen ongelma. Anna kaksi esimerkkiä NP-täydellisistä ongelmista ja osoita, että niiden välillä vallitsee polynominen palautusrelaatio. (Yhdensuuntainen palautus riittää, palautusekvivalenssia ei tarvitse osoittaa.)

Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.