TIE211 Tietorakenteet ja algoritmit 2
Kurssikoe ti 15.12.1998 8-12

1. Tietyn ongelman ratkaisemiseksi on tarjolla kaksi vaihtoehtoista menetelmää. Algoritmissa 1 ongelman tapaus, jonka koko on n, jaetaan kahteen n/2 kokoiseen osatapaukseen, jotka molemmat ratkaistaan rekursiivisesti. Tapauksen osittaminen ja osaratkaisujen yhdistäminen vaativat tässä menetelmässä n:n suhteen lineaarisen ajan. Algoritmissa 2 ongelman tapaus jaetaan n:n suhteen neliöllisessä ajassa kolmeen n/3 kokoiseen osatapaukseen, mutta näistä ratkaistaan rekursiivisesti vain yksi. Kumpi algoritmi on aikavaativuudeltaan asymptoottisesti tehokkaampi? (Perusteltu vastaus.)
2. Valuutta-arbitraasilla tarkoitetaan (yksinkertaistaen) valuuttojen vaihtosuhteiden erojen hyväksikäyttöä voittojen keräämiseen. Jos esimerkiksi yhdellä Suomen markalla saa 1,60 Ruotsin kruunua, yhdellä kruunulla 0,13 USA:n dollaria ja yhdellä dollarilla 5,00 markkaa, niin vaihtamalla markat ensin kruunuiksi, sitten kruunut dollareiksi ja dollarit takaisin markoiksi saa voittosuhteeksi 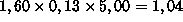. Suunnittele tehokas algoritmi, joka tutkii onko annetussa n valuutan valuuttakorissa, jossa valuutan i vaihtosuhde valuuttaa j vastaan on R[i,j], mahdollista harjoittaa voitollista arbitraasia. (Vihje: Floyd.)
3. Suunnittele algoritmi B(n,k), joka annetuilla syötteillä n ja k tuottaa ja tulostaa ne n bitin bittijonot, jotka sisältävät tasan k ykköstä. Algoritmin aikavaativuuden T(n,k) tulee olla verrannollinen tulostettujen bittijonojen määrään, so. on oltava 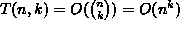(kiinteällä k). Esitä algoritmisi aikavaativuusanalyysi.
4. Määrittele seuraavat käsitteet: ongelmaluokka NP, polynominen palautus, NP-täydellinen ongelma. Anna kaksi esimerkkiä NP-täydellisistä ongelmista, perustele miksi ne kuuluvat luokkaan NP, ja osoita että niiden välillä vallitsee polynominen palautusrelaatio. (Yhdensuuntainen palautus riittää, palautusekvivalenssia ei tarvitse osoittaa.)

Pisteytys: Kukin tehtävä 15 pistettä, yhteensä 60 pistettä.