MAT282 Johdatus diskreettiin matematiikkaan (3 ov)
Loppukoe to 16.12.1999 klo 8-12

1. Korttipakassa on 52 korttia, jotka jakautuvat neljään ``maahan'' (hertta, ruutu, risti, pata). Kuhunkin maahan kuuluvat kortit on numeroitu 1,...,13.
   1. Montako erilaista viiden kortin ``pokerikättä'' (viiden kortin osajoukkoa) pakan korteista voidaan muodostaa? (Jos sinulla ei ole laskinta, kaava riittää vastaukseksi.)
   2. Monellako tavalla korteista voidaan muodostaa viiden kortin ``väri'', so. viiden kortin osajoukko jonka kaikki kortit ovat keskenään samaa maata?
   3. Monellako tavalla korteista voidaan muodostaa ``täyskäsi'', so. viiden kortin osajoukko joka koostuu ``kolmosista'' (kolme keskenään samanarvoista korttia) ja ``parista'' (kaksi keskenään samanarvoista korttia)? (Sama kortti ei tietenkään täyskädessä voi kuulua sekä kolmosiin että pariin.)
2. Joulupukki on päättänyt antaa jokaiselle matematiikan laitoksen seitsemästä professorista lahjaksi A. Sallisen esseekokoelman ``Tiedolla tulevaan'', ja joulumuori on juuri paketoimassa kirjoja. Muorilla on kullanväristä, punaista, sinistä ja vihreätä lahjapaperia, mutta kullanvärinen paperi riittää enintään kahteen ja punainen paperi enintään kolmeen pakettiin. Monellako eri tavalla muori voi paketoida nämä seitsemän keskenään identtistä lahjakirjaa?
3. Ratkaise rekursioyhtälö:

   

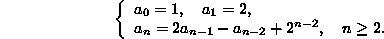
4. Pelimiehet Uuno ja Tauno pelaavat sanapeliä, jossa yhteisesti sovitusta n substantiivin joukosta muodostetaan vuorotellen yhdyssanoja niin, että seuraavaksi muodostettavan yhdyssanan alkuosa on aina sama kuin edellisen yhdyssanan loppuosa. Pelaajat ovat lisäksi sopineet, että jos sanat X ja Y on jo yhdistetty järjestyksessä XY, niin niitä ei saa enää yhdistää järjestyksessä YX. Uuno aloittaa pelin, ja se pelaaja, joka ensinnä ei pysty muodostamaan uutta yhdyssanaa, häviää. (Esimerkiksi jos sovittu sanajoukko on {JOULU, PORO, PUKKI}, niin yksi mahdollinen pelin kulku on seuraava. Uuno: ``JOULUPUKKI.'' Tauno: ``PUKKIPORO.'' Uuno: ``POROJOULU.'' Tauno: ``Hävisin.'') Todista, että jos sanojen määrä n on muotoa n = 4k+3, 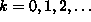, niin Uunolla on pelissä voittostrategia, so. voittoon johtavat siirtovalinnat. Kuvaile tämä strategia.
5. Tarkastellaan kuusibittistä lineaarista koodia, jonka tarkistusmatriisi on

   

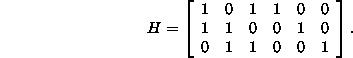
   1. Määritä koodin kaikki koodisanat.
   2. Määritä koodin etäisyys (engl. distance) ja teho (engl. rate).
   3. Esitä, miten tarkistusmatriisia H käyttäen määritetään yhden bittivirheen sisältävää jonoa 110110 vastaava kooodisana.

Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.