


Next: About this document
Up: No Title
Previous: No Title
-
Tiedekunnassa on dekaani ja yhdeksän muuta professoria: biologit
M, A ja T, fyysikot R ja P, kemistit V ja J sekä matemaatikot
K ja O. Dekaanin pitää muodostaa professoreista kehittämiskeskusteluja
varten ryhmiä. Kussakin ryhmässä voi olla useita professoreita,
kuitenkin seuraavin rajoituksin: kahta saman oppiaineen professoria
ei voi sijoittaa samaan ryhmään; professorit V ja T tulee sijoittaa
eri ryhmiin, samoin kuin professorit R ja M; professori A on ainoa
biologi jonka voi sijoittaa samaan ryhmään kummankaan matemaatikon
kanssa. Kukin kehittämiskeskustelu kestää tunnin. Muodosta dekaanin
avuksi jokin professoreiden ryhmittely, jota käyttäen hän selviää
keskusteluista mahdollisimman nopeasti. Montako tuntia vähintään
tarvitaan?
-
Dominopelin nappula on kahteen neliöön jaettu suorakaide,
jonka molemmissa puoliskoissa on nollasta kuuteen ``silmää''.
Jos pelistä jätetään pois nappulat, joiden puoliskojen
silmämäärä on sama, ja sovitaan että nappulan suunnistuksella
ei ole väliä, huomataan että dominonappulat vastaavat
täsmälleen kahden alkion joukkoja
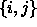 , missä
, missä
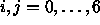 ,
, 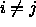 .
Osoita, että näin saatavat
.
Osoita, että näin saatavat 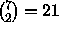 dominonappulaa voidaan asettaa dominopelin sääntöjen
mukaiseksi renkaaksi, jossa kahden toisiaan koskettavan
nappulan vastinpuoliskoissa on aina sama silmäluku.
Esimerkiksi oheisessa kuvassa on toistensa naapureiksi
laillisesti asetetut dominonappulat
dominonappulaa voidaan asettaa dominopelin sääntöjen
mukaiseksi renkaaksi, jossa kahden toisiaan koskettavan
nappulan vastinpuoliskoissa on aina sama silmäluku.
Esimerkiksi oheisessa kuvassa on toistensa naapureiksi
laillisesti asetetut dominonappulat 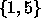 ja
ja 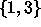 .
.

(Vihje: Tarkastele verkkoa 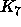 .)
.)
-
Kaikkien 15 EU-maan pääministerit saapuvat Jyväskylään huippukokoukseen
tapaamaan 15:ta Jyvässeudun merkittävää kunnallista vaikuttajaa. Kukin
pääministeri saa nimetä kolme vaikuttajaa, joiden kanssa hän
haluaisi neuvotella. Osoita, että mikäli kenellekään
jyvässeutulaiselle ei tule enempää kuin kolme neuvottelupyyntöä
(tällöin itse asiassa jokaiselle tulee tasan kolme),
kaikki toivotut tapaamiset voidaan järjestää kolmessa peräkkäisessä
vaiheessa, joissa kussakin käydään 15 pareittaista neuvottelua
EU:n ja Jyvässeudun edustajien kesken.
- Tarkastellaan viisinkertaista toistokoodia
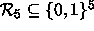 ,
jossa yksibittinen viesti
,
jossa yksibittinen viesti 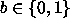 koodataan viisibittiseksi
jonoksi c(b) = bbbbb.
koodataan viisibittiseksi
jonoksi c(b) = bbbbb.
- Muodosta koodin koodisanat ja tarkistusmatriisi. Montako
virhettä koodi korjaa lähimmän naapurin periaatteella?
- Määritä koodin teho (engl. rate), ja osoita että koodi
on itse asiassa täydellinen (engl. perfect), so. omassa
luokassaan maksimaalisen tehokas.
- Määritä todennäköisyys, että koodia
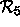 käyttäen koodattu viestisana b = 0 välittyy virheettömästi
kanavassa BSC(0.05), kun vastaanottaja käyttää lähimmän
naapurin dekoodausmenetelmää.
(Lisätieto niille, joiden todennäköisyyslaskennan
taidot ovat ruosteessa: ns. binomijakauman mukainen todennäköisyys
sille, että n-bittisessä viestissä sattuu tasan e virhettä on
käyttäen koodattu viestisana b = 0 välittyy virheettömästi
kanavassa BSC(0.05), kun vastaanottaja käyttää lähimmän
naapurin dekoodausmenetelmää.
(Lisätieto niille, joiden todennäköisyyslaskennan
taidot ovat ruosteessa: ns. binomijakauman mukainen todennäköisyys
sille, että n-bittisessä viestissä sattuu tasan e virhettä on
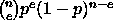 , kun yksittäisen virheen todennäköisyys
on p. Jos sinulla ei ole laskinta, myös symbolimuotoinen
virhetodennäköisyyden kaava kelpaa vastaukseksi.)
, kun yksittäisen virheen todennäköisyys
on p. Jos sinulla ei ole laskinta, myös symbolimuotoinen
virhetodennäköisyyden kaava kelpaa vastaukseksi.)
Pisteytys: kukin tehtävä á 9 pistettä, yhteensä 36 pistettä.



Next: About this document
Up: No Title
Previous: No Title
Pekka Orponen
Wed Nov 24 18:15:30 EET 1999
![]() .)
.) käyttäen koodattu viestisana b = 0 välittyy virheettömästi
kanavassa BSC(0.05), kun vastaanottaja käyttää lähimmän
naapurin dekoodausmenetelmää.
(Lisätieto niille, joiden todennäköisyyslaskennan
taidot ovat ruosteessa: ns. binomijakauman mukainen todennäköisyys
sille, että n-bittisessä viestissä sattuu tasan e virhettä on
käyttäen koodattu viestisana b = 0 välittyy virheettömästi
kanavassa BSC(0.05), kun vastaanottaja käyttää lähimmän
naapurin dekoodausmenetelmää.
(Lisätieto niille, joiden todennäköisyyslaskennan
taidot ovat ruosteessa: ns. binomijakauman mukainen todennäköisyys
sille, että n-bittisessä viestissä sattuu tasan e virhettä on
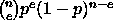 , kun yksittäisen virheen todennäköisyys
on p. Jos sinulla ei ole laskinta, myös symbolimuotoinen
virhetodennäköisyyden kaava kelpaa vastaukseksi.)
, kun yksittäisen virheen todennäköisyys
on p. Jos sinulla ei ole laskinta, myös symbolimuotoinen
virhetodennäköisyyden kaava kelpaa vastaukseksi.)