


Next: About this document
Up: No Title
Previous: No Title
-
- Kuinka monta lehteä voi (i) enintään, (ii) vähintään
olla n-solmuisessa puussa? (Pelkkä vastaus riittää, ei
tarvitse todistaa.)
- Piirrä kaikki keskenään ei-isomorfiset nelilehtiset,
enintään 7-solmuiset puut.
-
Olkoon G = (V,E) (suuntaamaton) verkko, jonka jokaisen solmun asteluku
on parillinen. Osoita, että G:n kaaret voidaan suunnata niin,
että syntyvässä suhteikossa ovat kunkin solmun tulo- ja lähtöaste
(= tulevien ja lähtevien kaarien määrä) keskenään yhtä suuret.
-
- Olkoon G = (V,E) vähintään 3-solmuinen yhtenäinen tasoverkko,
jonka kaikki syklit ovat vähintään neljän pituisia
(so. verkko ei sisällä
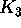 -muotoista indusoitua aliverkkoa
eli on kolmioton).
Osoita, että G:n kaarien määrää rajoittaa tällöin epäyhtälö
-muotoista indusoitua aliverkkoa
eli on kolmioton).
Osoita, että G:n kaarien määrää rajoittaa tällöin epäyhtälö
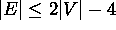 . (Kuten luennolla esitettiin,
ilman kolmiottomuusoletusta saadaan heikompi
epäyhtälö
. (Kuten luennolla esitettiin,
ilman kolmiottomuusoletusta saadaan heikompi
epäyhtälö 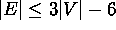 .)
.) - Osoita edellisen tuloksen nojalla, että verkko
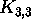 ei ole planaarinen.
ei ole planaarinen.
- Tarkastellaan 15-bittistä Hamming-koodia
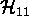 (11 viestibittiä, 4 pariteettibittiä, 1 virheen korjaus).
(11 viestibittiä, 4 pariteettibittiä, 1 virheen korjaus).
- Esitä koodin tarkistusmatriisi, jonka
sarakkeet on lueteltu luonnollisessa järjestyksessä.
- Montako koodisanaa koodissa on?
- Määritä koodin teho (engl. rate).
- Osoita, että missään 15-bittisessä, 1 virheen korjaavassa
koodissa ei voi olla enempää koodisanoja kuin koodissa
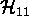 ,
ja se on siten tässä koodiluokassa maksimaalisen tehokas.
,
ja se on siten tässä koodiluokassa maksimaalisen tehokas. - Anna jokin kelvollinen koodisana
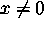 ja vahvista,
että todella on
ja vahvista,
että todella on 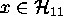 .
. - Määritä yhden bittivirheen sisältävää jonoa 011101110011011
vastaava kelvollinen koodisana.
Pisteytys: kukin tehtävä á 9 pistettä, yhteensä 36 pistettä.
Pekka Orponen
Thu Nov 18 00:30:01 EET 1999
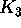 -muotoista indusoitua aliverkkoa
eli on kolmioton).
Osoita, että G:n kaarien määrää rajoittaa tällöin epäyhtälö
-muotoista indusoitua aliverkkoa
eli on kolmioton).
Osoita, että G:n kaarien määrää rajoittaa tällöin epäyhtälö
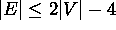 . (Kuten luennolla esitettiin,
ilman kolmiottomuusoletusta saadaan heikompi
epäyhtälö
. (Kuten luennolla esitettiin,
ilman kolmiottomuusoletusta saadaan heikompi
epäyhtälö 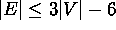 .)
.)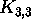 ei ole planaarinen.
ei ole planaarinen.
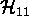 ,
ja se on siten tässä koodiluokassa maksimaalisen tehokas.
,
ja se on siten tässä koodiluokassa maksimaalisen tehokas.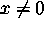 ja vahvista,
että todella on
ja vahvista,
että todella on 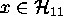 .
.