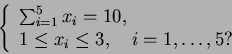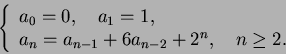Next: Tästä dokumentista ...
Up: vk_991020
Previous: vk_991020
- Luettele kaikki joukon
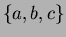 ositukset
(ekvivalenssirelaatiot). Montako ositusta voidaan yleisesti
muodostaa
ositukset
(ekvivalenssirelaatiot). Montako ositusta voidaan yleisesti
muodostaa 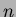 alkion joukossa?
alkion joukossa?
- Olkoon
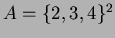 . Piirrä Hasse-kaavio järjestysrelaatiosta
. Piirrä Hasse-kaavio järjestysrelaatiosta
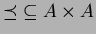 , missä
, missä
(Merkintä 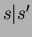 tarkoittaa, että kokonaisluku
tarkoittaa, että kokonaisluku 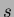 on
kokonaisluvun
on
kokonaisluvun 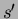 tekijä.)
tekijä.)
- Kuinka monta sellaista viisimerkkistä ``sanaa'' voidaan muodostaa
aakkoston {A, E, M, N, S} kirjaimista, joissa kirjain A esiintyy
kaksi tai kolme kertaa ja kukin muista kirjaimista enintään kerran?
Sanojen ei tarvitse olla suomenkielen äänneopin mukaisia: kelvollisia
ovat siis esimerkiksi AAMEN, ASEMA ja AMSAA, mutta eivät MENSA eikä
MASSA.
- Montako kokonaislukuratkaisua on epäyhtälöryhmällä:
- Kokeessa on viisi monivalintatehtävää, joissa on kussakin
viisi ratkaisuvaihtoehtoa (a,...,e). Opiskelija
K tietää, että kaikkiin kysymyksiin on vastattava eri
tavalla, mutta muuten hänellä ei ole mitään käsitystä oikeista
vastauksista. Monellako tavalla K voi muodostaa vastausrivin
niin, että siinä ovat kaikki vastaukset väärin?
(Vihje: Tarkastele, monellako tavalla vastausrivin
voisi muodostaa niin, että siinä olisi ainakin
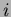 .
vastaus oikein,
.
vastaus oikein, 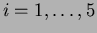 .)
.)
- Ratkaise rekursioyhtälö:
Pisteytys: tehtävät 1 ja 2 á 8 pistettä, tehtävät 3 ja 4
á 7 pistettä, yhteensä 30 pistettä.



Next: Tästä dokumentista ...
Up: vk_991020
Previous: vk_991020
Pekka Orponen
2000-10-19
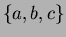 ositukset
(ekvivalenssirelaatiot). Montako ositusta voidaan yleisesti
muodostaa
ositukset
(ekvivalenssirelaatiot). Montako ositusta voidaan yleisesti
muodostaa 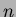 alkion joukossa?
alkion joukossa?
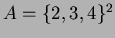 . Piirrä Hasse-kaavio järjestysrelaatiosta
. Piirrä Hasse-kaavio järjestysrelaatiosta
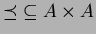 , missä
, missä

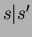 tarkoittaa, että kokonaisluku
tarkoittaa, että kokonaisluku 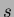 on
kokonaisluvun
on
kokonaisluvun 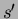 tekijä.)
tekijä.)