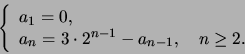Next: Tästä dokumentista ...
Up: lk_010613
Previous: lk_010613
- Järvi-Suomen yliopiston Kombinaatioteknologian tiedekunnassa
on viisi vakinaista professoria, jotka tiedekunnan
organisaatiouudistuksen yhteydessä uudelleensijoitellaan
tiedekunnan kolmeen laitokseen niin, että kullekin laitokselle
tulee vähintään yksi vakinainen professori. Monellako tavalla
sijoittelu voidaan tehdä, kun professorit ovat (a) keskenään
identtisiä, (b) toisistaan erottuvia? (Laitokset ovat
kummassakin tapauksessa ei-identtisiä.)
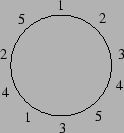
- Kuvassa 1 on kokonaisluvut
 sijoitettu
ympyrän kehälle niin, että kukin luku esiintyy toisen
naapurina tasan yhden kerran. Osoita, että tällainen
kokonaislukujen
sijoitettu
ympyrän kehälle niin, että kukin luku esiintyy toisen
naapurina tasan yhden kerran. Osoita, että tällainen
kokonaislukujen  sijoittelu on mahdollinen
aina ja vain kun
sijoittelu on mahdollinen
aina ja vain kun 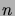 on pariton. (Vihje: Tarkastele
verkkoa
on pariton. (Vihje: Tarkastele
verkkoa 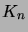 .)
.)
Kuva 1:
Lukuympyrä
 |
- Vuoden 2003 eduskuntavaalien jälkeen koottavaan
laajapohjaiseen Kansalliseen Konsensushallitukseen
nimitetään kaikkiaan 18 ministeriä viidestä suurimmasta
puolueesta. Monellako tavalla hallitus voidaan koota,
kun kustakin puolueesta halutaan mukaan
vähintään kaksi, mutta enintään viisi ministeriä?
(Ministeripaikat ja saman puolueen ministerit ovat
keskenään samanveroisia; vain lukumäärillä on merkitystä.)
- Ratkaise rekursioyhtälö:
- Tunnetussa susi, lammas ja kaalinpää -ongelmassa
miehen pitää kuljettaa mainitut kolme hahmoa veneellä
joen yli, mutta veneeseen mahtuu miehen kanssa yhtä aikaa
vain yksi kuljetettava. Sutta ja lammasta ei saa jättää
kahdestaan samalle rannalle, samoin kuin ei lammasta ja
kaalinpäätä. Mallinna ongelma verkkoteoreettisesti ja
määritä tältä pohjalta, montako kertaa mies vähintään
joutuu soutamaan joen poikki, sekä montako erilaista
``minimisouturatkaisua'' hänellä on valittavanaan.
(Huom. 1. Myös paluusoudut lasketaan mukaan ylityksiin,
joten tarvittavien ylitysten määrä on triviaalisti ainakin
seitsemän. Huom. 2. Esitettävän ratkaisun täytyy
perustua muodostettuun ongelman verkkomalliin. Toisiinsa
liittymätön verkko ja ``intuitiivinen'' ratkaisu eivät
kelpaa vastaukseksi.)
Pisteytys: Kukin tehtävä 12 pistettä, yhteensä 60 pistettä.



Next: Tästä dokumentista ...
Up: lk_010613
Previous: lk_010613
Pekka Orponen
2001-06-13